【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 是
是![]() 上一点,直线
上一点,直线![]() 与抛物线交于
与抛物线交于![]() 两点,若
两点,若![]() ,则
,则![]() ( )
( )
A. ![]() B. 8 C. 16 D.
B. 8 C. 16 D. ![]()
参考答案:
【答案】A
【解析】分析:利用抛物线性质分析线段比,进而得直线斜率,写出直线的方程,再将直线的方程与抛物线y2=4x的方程组成方程组,消去y得到关于x的二次方程,最后利用根与系数的关系结合抛物线的定义即可求线段MN的长.
详解:抛物线C:![]() 的焦点为F(1,0),准线为l:x=﹣1,
的焦点为F(1,0),准线为l:x=﹣1,![]() 与x轴交于点Q
与x轴交于点Q
设M(x1,y1),N(x2,y2),M,N到准线的距离分别为dM,dN,
由抛物线的定义可知|MF|=dM=x1+1,|NF|=dN=x2+1,于是|MN|=|MF|+|NF|=x1+x2+2.
∵![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() .
.
∴![]() ,∴直线AB的斜率为
,∴直线AB的斜率为![]() ,
,
∵F(1,0),∴直线PF的方程为y=![]() (x﹣1),
(x﹣1),
将y=![]() (x﹣1),代入方程y2=4x,得3(x﹣1)2=4x,化简得3x2﹣10x+3=0,
(x﹣1),代入方程y2=4x,得3(x﹣1)2=4x,化简得3x2﹣10x+3=0,
∴x1+x2=![]() ,于是|MN|=|MF|+|NF|=x1+x2+2=
,于是|MN|=|MF|+|NF|=x1+x2+2=![]() +2=
+2=![]() .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
, ,
, 均为正的常数)的最小正周期为
均为正的常数)的最小正周期为 ,当
,当 时,函数
时,函数 取得最小值,则下列结论正确的是( )
取得最小值,则下列结论正确的是( )A.

B.

C.

D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,任取
,任取 ,若函数
,若函数 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 ,记
,记 .
.(1)求函数
 的最小正周期及对称轴方程;
的最小正周期及对称轴方程;(2)当
 时,求函数
时,求函数 的解析式;
的解析式;(3)设函数
 ,
, ,其中
,其中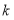 为参数,且满足关于
为参数,且满足关于 的不等式
的不等式 有解,若对任意
有解,若对任意 ,存在
,存在 ,使得
,使得 成立,求实数
成立,求实数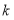 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=
 (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为 ,弦长为
,弦长为 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中 ,
, )
)A. 15 B. 16 C. 17 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,讨论函数
时,讨论函数 的单调性;
的单调性;(2)当
 时,对于任意正实数
时,对于任意正实数 ,不等式
,不等式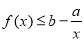 恒成立,试判断实数
恒成立,试判断实数 的大小关系.
的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
,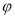 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 ,若直线
,若直线 与曲线
与曲线 相切;
相切; (1)求曲线
 的极坐标方程与直线
的极坐标方程与直线 的直角坐标方程;
的直角坐标方程;(2)在曲线
 上取两点
上取两点 ,
, 与原点
与原点 构成
构成 ,且满足
,且满足 ,求
,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,直线
,直线 ,在圆
,在圆 内任取一点
内任取一点 ,则
,则 到直线的距离大于2的概率为__________.
到直线的距离大于2的概率为__________.
相关试题

