【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过
不超过![]() 尾/立方米时,
尾/立方米时, ![]() 的值为
的值为![]() 千克/年;当
千克/年;当![]() 时,
时, ![]() 是
是![]() 的一次函数,且当
的一次函数,且当![]() 时,
时, ![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 关于
关于![]() 的函数的表达式.
的函数的表达式.
(![]() )当养殖密度
)当养殖密度![]() 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
参考答案:
【答案】(1)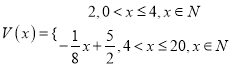 (2)当养殖密度为
(2)当养殖密度为![]() 尾/立方米时,鱼的年生长量可以达到最大,最大值约为
尾/立方米时,鱼的年生长量可以达到最大,最大值约为![]() 千克/立方米.
千克/立方米.
【解析】试题分析:(1)根据题意分段求解析式,利用待定系数法求一次函数解析式,最后按分段函数形式书写(2)按一次函数与二次函数性质分别求最大值,最后取两者最大值
试题解析:(![]() )当
)当![]() 时,
时, ![]() ;当
;当![]() 时,
时,
设![]() ,显然该函数的区间
,显然该函数的区间![]() 上是减函数,
上是减函数,
由已知得![]() ,解得
,解得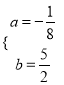 ,
,
故函数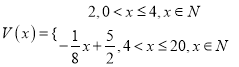 .
.
(![]() )依题意并由(
)依题意并由(![]() )可得
)可得
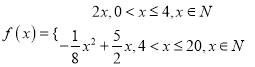 ,
,
当![]() 时,
时, ![]() 为增函数,故
为增函数,故![]() ;
;
当![]() 时,
时, ![]() ,
,
![]() .
.
所以,当![]() 时,
时, ![]() 的最大值为
的最大值为![]() .
.
当养殖密度为![]() 尾/立方米时,鱼的年生长量可以达到最大,
尾/立方米时,鱼的年生长量可以达到最大,
最大值约为![]() 千克/立方米.
千克/立方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题
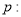 方程
方程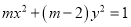 表示双曲线;命题
表示双曲线;命题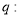 不等式
不等式 的解集是
的解集是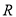 .
. 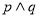 为假,
为假, 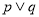 为真,求
为真,求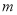 的取值范围.
的取值范围.【答案】

【解析】试题分析:由命题
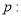 方程
方程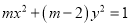 表示双曲线,求出
表示双曲线,求出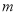 的取值范围,由命题
的取值范围,由命题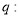 不等式
不等式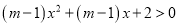 的解集是
的解集是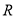 ,求出
,求出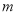 的取值范围,由
的取值范围,由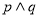 为假,
为假, 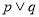 为真,得出
为真,得出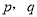 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出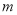 的取值范围.
的取值范围.试题解析:
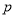 真
真 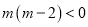
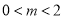 ,
,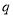 真
真 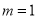 或
或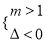

∴
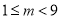
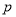 真
真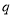 假
假 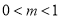
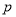 假
假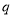 真
真 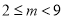
∴
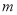 范围为
范围为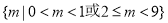
【题型】解答题
【结束】
18【题目】如图,设
 是圆
是圆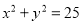 上的动点,点
上的动点,点 是
是 在
在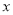 轴上的投影,
轴上的投影, 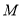 为
为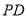 上一点,且
上一点,且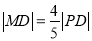 .
.
(1)当
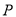 在圆上运动时,求点
在圆上运动时,求点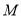 的轨迹
的轨迹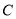 的方程;
的方程;(2)求过点
 且斜率为
且斜率为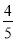 的直线被
的直线被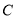 所截线段的长度.
所截线段的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若对任意的
,若对任意的 ,总存在
,总存在 ,使得
,使得 ,则实数
,则实数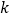 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D. 以上都不对
D. 以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
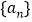 的前
的前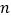 项和为
项和为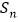 ,等比数列
,等比数列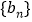 的前
的前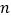 项和为
项和为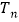 ,且
,且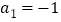 ,
,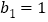 ,
,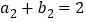 .
.(1)若
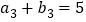 ,求
,求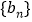 的通项公式;
的通项公式;(2)若
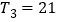 ,求
,求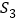 .
.【答案】(1)
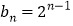 ;(2)21或
;(2)21或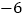 .
.【解析】试题分析:(1)设等差数列
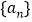 公差为
公差为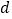 ,等比数列
,等比数列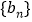 公比为
公比为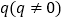 ,由已知条件求出
,由已知条件求出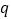 ,再写出通项公式;(2)由
,再写出通项公式;(2)由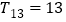 ,求出
,求出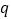 的值,再求出
的值,再求出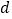 的值,求出
的值,求出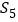 。
。试题解析:设等差数列
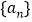 公差为
公差为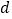 ,等比数列
,等比数列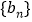 公比为
公比为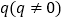 有
有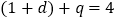 ,即
,即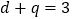 .
.(1)∵
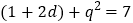 ,结合
,结合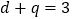 得
得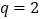 ,
,∴
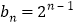 .
.(2)∵
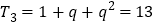 ,解得
,解得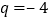 或3,
或3,当
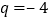 时,
时,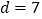 ,此时
,此时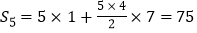 ;
;当
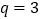 时,
时,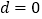 ,此时
,此时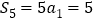 .
.【题型】解答题
【结束】
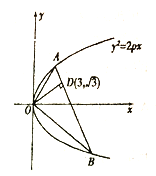
20【题目】如图,已知直线与抛物线
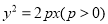 相交于
相交于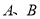 两点,且
两点,且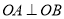 ,
, 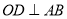 交
交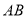 于
于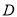 ,且点
,且点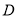 的坐标为
的坐标为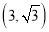 .
.
(1)求
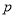 的值;
的值;(2)若
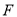 为抛物线的焦点,
为抛物线的焦点, 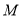 为抛物线上任一点,求
为抛物线上任一点,求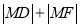 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)若
 ,求方程
,求方程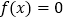 的解;
的解;(2)若关于x的方程
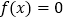 在(0,2)上有两个解
在(0,2)上有两个解 ,求k的取值范围,并证明
,求k的取值范围,并证明 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 ,则下列结论错误的是( )
,则下列结论错误的是( )A.
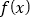 是偶函数 B.
是偶函数 B. 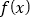 的值域是
的值域是
C. 方程
 的解只有
的解只有 D. 方程
D. 方程 的解只有
的解只有
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在
在 和
和 处取得极值.
处取得极值.(1)求f(x)的表达式和极值.
(2)若f(x)在区间[m,m+4]上是单调函数,试求m的取值范围.
相关试题

