【题目】命题![]() 方程
方程![]() 表示双曲线;命题
表示双曲线;命题![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 为假,
为假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:由命题![]() 方程
方程![]() 表示双曲线,求出
表示双曲线,求出![]() 的取值范围,由命题
的取值范围,由命题![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范围,由
的取值范围,由![]() 为假,
为假, ![]() 为真,得出
为真,得出![]() 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出![]() 的取值范围.
的取值范围.
试题解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范围为
范围为![]()
【题型】解答题
【结束】
18
【题目】如图,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是
是![]() 在
在![]() 轴上的投影,
轴上的投影, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.

(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)求过点![]() 且斜率为
且斜率为![]() 的直线被
的直线被![]() 所截线段的长度.
所截线段的长度.
参考答案:
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】试题分析:(1)由题意可知:M的坐标为(x,y),P的坐标为(x',y'),则![]() ,得
,得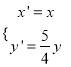 ,代入
,代入![]() ,整理得:
,整理得: ![]() .
.
(2)设直线方程为: ![]() ,代入椭圆方程,由韦达定理可知:x1+x2=3,x1x2=-8,弦长公式:丨AB丨=
,代入椭圆方程,由韦达定理可知:x1+x2=3,x1x2=-8,弦长公式:丨AB丨=![]() 即可求得直线被C所截线段的长度.
即可求得直线被C所截线段的长度.
试题解析:
(1)设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,由已知得
,由已知得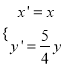 .
.
∵![]() 在圆上,
在圆上, ![]() ,
,
即![]() ,整理得
,整理得![]() ,即
,即![]() 的方程为
的方程为![]() .
.
(2)过点![]() 且斜率为
且斜率为![]() 的直线方程为
的直线方程为![]() ,
,
设直线与![]() 的交点为
的交点为![]() ,
, ![]() ,将直线方程
,将直线方程![]() 代入
代入![]() 的方程,
的方程,
得![]() ,即
,即![]() .
.
∴x1+x2=3,x1x2=-8∴线段![]() 的长度为
的长度为
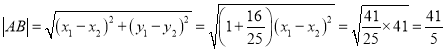 .
.
∴直线被![]() 所截线段的长度为
所截线段的长度为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 中,公差
中,公差  ,
,  ,且
,且  成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)若 为数列
为数列  的前
的前  项和,且存在
项和,且存在  ,使得
,使得 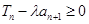 成立,求实数
成立,求实数  的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
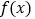 图象如图,
图象如图,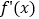 是
是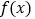 的导函数,则下列数值排序正确的是( )
的导函数,则下列数值排序正确的是( )
A.
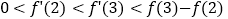
B.

C.
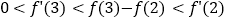
D.

【答案】C
【解析】结合函数的图像可知过点
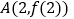 的切线的倾斜角最大,过点
的切线的倾斜角最大,过点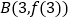 的切线的倾斜角最小,又因为点
的切线的倾斜角最小,又因为点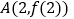 的切线的斜率
的切线的斜率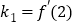 ,点
,点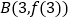 的切线斜率
的切线斜率 ,直线
,直线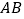 的斜率
的斜率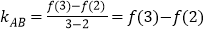 ,故
,故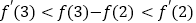 ,应选答案C。
,应选答案C。点睛:本题旨在考查导数的几何意义与函数的单调性等基础知识的综合运用。求解时充分借助题设中所提供的函数图形的直观,数形结合进行解答。先将经过两切点
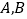 的直线绕点
的直线绕点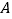 逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点
逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点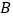 顺时针旋转到与函数的图像相切,这个过程很容易发现
顺时针旋转到与函数的图像相切,这个过程很容易发现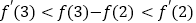 ,从而将问题化为直观图形的问题来求解。
,从而将问题化为直观图形的问题来求解。【题型】单选题
【结束】
9【题目】已知
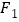 、
、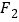 为双曲线
为双曲线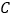 :
: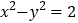 的左、右焦点,点
的左、右焦点,点 在
在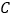 上,
上,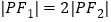 ,则
,则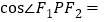 ( )
( )A.
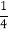 B.
B.  C.
C. 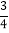 D.
D. 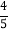
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)为一次函数,g(x)为二次函数,且f[g(x)]=g[f(x)].
(1)求f(x)的解析式;
(2)若y=g(x)与x轴及y=f(x)都相切,且g(0)=
 ,求g(x)的解析式.
,求g(x)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若对任意的
,若对任意的 ,总存在
,总存在 ,使得
,使得 ,则实数
,则实数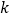 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D. 以上都不对
D. 以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
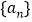 的前
的前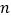 项和为
项和为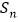 ,等比数列
,等比数列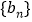 的前
的前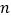 项和为
项和为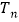 ,且
,且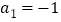 ,
,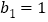 ,
,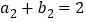 .
.(1)若
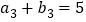 ,求
,求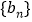 的通项公式;
的通项公式;(2)若
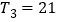 ,求
,求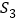 .
.【答案】(1)
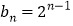 ;(2)21或
;(2)21或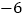 .
.【解析】试题分析:(1)设等差数列
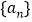 公差为
公差为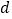 ,等比数列
,等比数列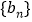 公比为
公比为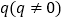 ,由已知条件求出
,由已知条件求出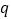 ,再写出通项公式;(2)由
,再写出通项公式;(2)由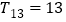 ,求出
,求出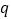 的值,再求出
的值,再求出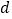 的值,求出
的值,求出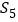 。
。试题解析:设等差数列
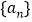 公差为
公差为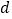 ,等比数列
,等比数列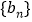 公比为
公比为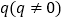 有
有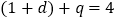 ,即
,即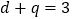 .
.(1)∵
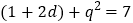 ,结合
,结合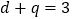 得
得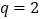 ,
,∴
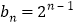 .
.(2)∵
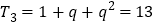 ,解得
,解得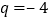 或3,
或3,当
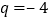 时,
时,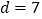 ,此时
,此时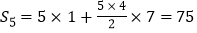 ;
;当
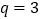 时,
时,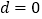 ,此时
,此时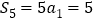 .
.【题型】解答题
【结束】
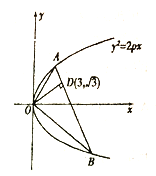
20【题目】如图,已知直线与抛物线
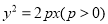 相交于
相交于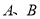 两点,且
两点,且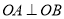 ,
, 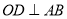 交
交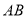 于
于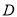 ,且点
,且点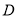 的坐标为
的坐标为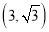 .
.
(1)求
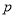 的值;
的值;(2)若
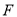 为抛物线的焦点,
为抛物线的焦点, 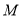 为抛物线上任一点,求
为抛物线上任一点,求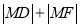 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度
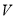 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度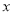 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当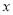 不超过
不超过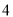 尾/立方米时,
尾/立方米时, 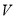 的值为
的值为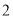 千克/年;当
千克/年;当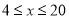 时,
时, 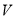 是
是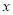 的一次函数,且当
的一次函数,且当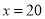 时,
时, 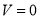 .
.(
 )当
)当 时,求
时,求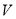 关于
关于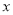 的函数的表达式.
的函数的表达式.(
 )当养殖密度
)当养殖密度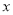 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
相关试题

