【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】试题分析:(1)设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() ,由已知条件求出
,由已知条件求出![]() ,再写出通项公式;(2)由
,再写出通项公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
试题解析:设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,结合
,结合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
【题型】解答题
【结束】
20
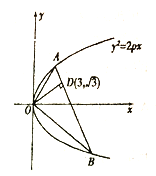
【题目】如图,已知直线与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 为抛物线上任一点,求
为抛物线上任一点,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)![]() .(2)4.
.(2)4.
【解析】试题分析:(1)设A(x1,y1),B(x2,y2),由AB⊥OD,kOD=![]() ,可得直线AB的斜率k=-
,可得直线AB的斜率k=-![]() ,得到直线AB的方程为
,得到直线AB的方程为![]() ,与抛物线方程联立化为
,与抛物线方程联立化为![]() ∴
∴![]() ,由
,由![]() 得
得![]() ,即
,即![]() ,∴
,∴![]() ,即可解得
,即可解得![]() 的值;
的值;
(2)过点M作直线的垂线MN,垂足为N,则|MF|=|MN|,由抛物线定义知![]() 的最小值为
的最小值为![]() 点到抛物线
点到抛物线![]() 准线的距离.
准线的距离.
试题解析:
(1)设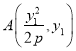 ,
, 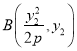 ,
, ![]() ,
,
则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
即![]() .将
.将![]() 代入上式,
代入上式,
整理得![]() ,∴
,∴![]() ,由
,由![]() 得
得![]() ,即
,即
![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() .
.
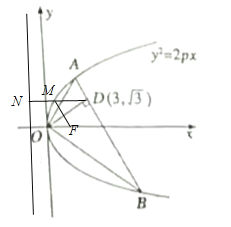
(2)过点M作直线的垂线MN,垂足为N,则|MF|=|MN|,由抛物线定义知![]() 的最小值为
的最小值为![]() 点到抛物线
点到抛物线![]() 准线的距离,又准线方程为
准线的距离,又准线方程为![]() ,因此
,因此![]() 的最小值为DN=4.
的最小值为DN=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)为一次函数,g(x)为二次函数,且f[g(x)]=g[f(x)].
(1)求f(x)的解析式;
(2)若y=g(x)与x轴及y=f(x)都相切,且g(0)=
 ,求g(x)的解析式.
,求g(x)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】命题
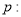 方程
方程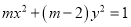 表示双曲线;命题
表示双曲线;命题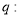 不等式
不等式 的解集是
的解集是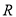 .
. 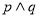 为假,
为假, 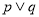 为真,求
为真,求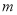 的取值范围.
的取值范围.【答案】

【解析】试题分析:由命题
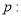 方程
方程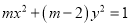 表示双曲线,求出
表示双曲线,求出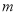 的取值范围,由命题
的取值范围,由命题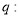 不等式
不等式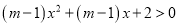 的解集是
的解集是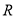 ,求出
,求出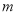 的取值范围,由
的取值范围,由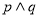 为假,
为假, 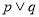 为真,得出
为真,得出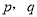 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出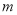 的取值范围.
的取值范围.试题解析:
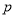 真
真 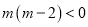
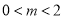 ,
,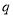 真
真 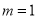 或
或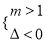

∴
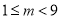
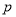 真
真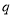 假
假 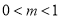
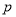 假
假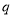 真
真 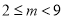
∴
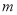 范围为
范围为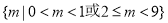
【题型】解答题
【结束】
18【题目】如图,设
 是圆
是圆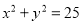 上的动点,点
上的动点,点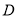 是
是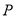 在
在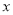 轴上的投影,
轴上的投影, 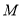 为
为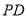 上一点,且
上一点,且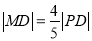 .
.
(1)当
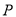 在圆上运动时,求点
在圆上运动时,求点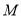 的轨迹
的轨迹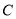 的方程;
的方程;(2)求过点
 且斜率为
且斜率为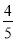 的直线被
的直线被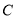 所截线段的长度.
所截线段的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若对任意的
,若对任意的 ,总存在
,总存在 ,使得
,使得 ,则实数
,则实数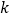 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D. 以上都不对
D. 以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度
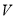 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度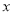 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当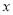 不超过
不超过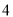 尾/立方米时,
尾/立方米时, 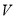 的值为
的值为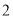 千克/年;当
千克/年;当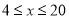 时,
时, 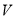 是
是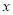 的一次函数,且当
的一次函数,且当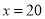 时,
时, 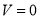 .
.(
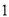 )当
)当 时,求
时,求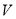 关于
关于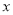 的函数的表达式.
的函数的表达式.(
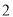 )当养殖密度
)当养殖密度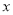 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)若
 ,求方程
,求方程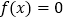 的解;
的解;(2)若关于x的方程
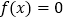 在(0,2)上有两个解
在(0,2)上有两个解 ,求k的取值范围,并证明
,求k的取值范围,并证明 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 ,则下列结论错误的是( )
,则下列结论错误的是( )A.
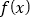 是偶函数 B.
是偶函数 B. 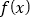 的值域是
的值域是
C. 方程
 的解只有
的解只有 D. 方程
D. 方程 的解只有
的解只有
相关试题

