【题目】已知![]() .
.
(1)若![]() ,求方程
,求方程![]() 的解;
的解;
(2)若关于x的方程![]() 在(0,2)上有两个解
在(0,2)上有两个解![]() ,求k的取值范围,并证明
,求k的取值范围,并证明![]() .
.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)k的取值范围为
;(2)k的取值范围为![]() ,证明见解析。
,证明见解析。
【解析】
(1)当k=2时,f(x)=|x2﹣1|+x2+2x=0,下面分两种情况讨论:①当x2﹣1≥0,②当x2﹣1<0,分别解出方程f(x)=0的解即可;
(2)不妨设0<x1<x2<2,因为![]() ,所以f(x)在(0,1]上是单调函数,故f(x)=0在(0,1]上至多一个解,结合根的范围求出当
,所以f(x)在(0,1]上是单调函数,故f(x)=0在(0,1]上至多一个解,结合根的范围求出当![]() 时,方程f(x)=0在(0,2)上有两个解,下面求
时,方程f(x)=0在(0,2)上有两个解,下面求![]() 的取值范围,先得出则
的取值范围,先得出则![]() 关于k的函数,再利用函数的单调性求其范围.
关于k的函数,再利用函数的单调性求其范围.
(1)当k=2时,![]() ,
,
①当![]() ,即x≥1或x≤-1时,
,即x≥1或x≤-1时,
方程化为![]() ,解得
,解得![]() ,
,
因为![]() ,舍去,所以
,舍去,所以![]() ;
;
②当![]() ,即-1<x<1时,方程化为2x+1=0,解得:
,即-1<x<1时,方程化为2x+1=0,解得:![]() ;
;
由①②得,当k=2时,方程f(x)=0的解为![]() 或
或![]() 。
。
(2)不妨设![]() ,
,
因为 ,
,
所以f(x)在(0,1]是单调函数,故f(x)=0在(0,1]上至多一个解,
若![]() ,则
,则![]() <0,故不符题意,
<0,故不符题意,
因此![]() ;
;
由![]() ,得
,得![]() ,所以k≤-1;
,所以k≤-1;
由![]() ,得
,得![]() ,所以
,所以![]() ;
;
故当![]() 时,方程f(x)=0在(0,2)上有两个解;
时,方程f(x)=0在(0,2)上有两个解;
因为![]() ,所以
,所以![]() ,
,![]() ,
,
消去k,得![]() ,
,
即![]() ,
,
因为x2<2,
所以![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若对任意的
,若对任意的 ,总存在
,总存在 ,使得
,使得 ,则实数
,则实数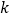 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D. 以上都不对
D. 以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
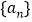 的前
的前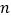 项和为
项和为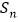 ,等比数列
,等比数列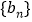 的前
的前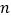 项和为
项和为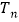 ,且
,且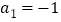 ,
,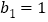 ,
,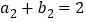 .
.(1)若
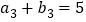 ,求
,求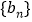 的通项公式;
的通项公式;(2)若
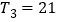 ,求
,求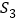 .
.【答案】(1)
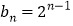 ;(2)21或
;(2)21或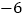 .
.【解析】试题分析:(1)设等差数列
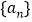 公差为
公差为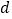 ,等比数列
,等比数列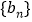 公比为
公比为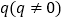 ,由已知条件求出
,由已知条件求出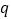 ,再写出通项公式;(2)由
,再写出通项公式;(2)由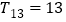 ,求出
,求出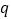 的值,再求出
的值,再求出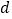 的值,求出
的值,求出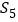 。
。试题解析:设等差数列
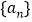 公差为
公差为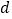 ,等比数列
,等比数列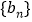 公比为
公比为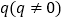 有
有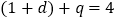 ,即
,即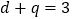 .
.(1)∵
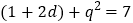 ,结合
,结合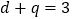 得
得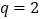 ,
,∴
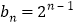 .
.(2)∵
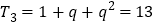 ,解得
,解得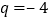 或3,
或3,当
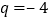 时,
时,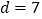 ,此时
,此时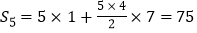 ;
;当
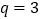 时,
时,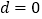 ,此时
,此时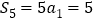 .
.【题型】解答题
【结束】
20【题目】如图,已知直线与抛物线
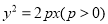 相交于
相交于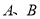 两点,且
两点,且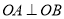 ,
, 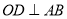 交
交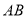 于
于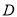 ,且点
,且点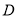 的坐标为
的坐标为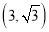 .
.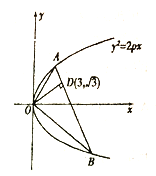
(1)求
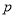 的值;
的值;(2)若
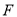 为抛物线的焦点,
为抛物线的焦点, 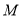 为抛物线上任一点,求
为抛物线上任一点,求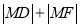 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度
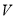 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度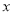 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当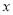 不超过
不超过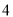 尾/立方米时,
尾/立方米时, 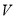 的值为
的值为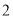 千克/年;当
千克/年;当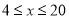 时,
时, 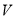 是
是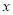 的一次函数,且当
的一次函数,且当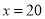 时,
时, 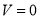 .
.(
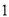 )当
)当 时,求
时,求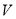 关于
关于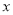 的函数的表达式.
的函数的表达式.(
 )当养殖密度
)当养殖密度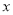 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 ,则下列结论错误的是( )
,则下列结论错误的是( )A.
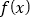 是偶函数 B.
是偶函数 B. 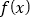 的值域是
的值域是
C. 方程
 的解只有
的解只有 D. 方程
D. 方程 的解只有
的解只有
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在
在 和
和 处取得极值.
处取得极值.(1)求f(x)的表达式和极值.
(2)若f(x)在区间[m,m+4]上是单调函数,试求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
相关试题

