【题目】某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示。
,得到的频率分布直方图如图所示。

(1)求第3、4、5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率。
参考答案:
【答案】(1)0.1;(2)第3、4、5组分别抽取3人、2人、1人;(3)![]() .
.
【解析】
本试题主要是考查了直方图的性质的运用,以及古典概型概率的运算的综合运用。
(1)由题设可知,第![]() 组的频率为
组的频率为![]() 第
第![]() 组的频率为
组的频率为![]()
第![]() 组的频率为
组的频率为![]() 。
。
(2)第![]() 组的人数为
组的人数为![]() 第
第![]() 组的人数为
组的人数为![]()
第![]() 组的人数为
组的人数为![]() 。利用分层抽样的等比例性质得到各层应该抽取的人数。
。利用分层抽样的等比例性质得到各层应该抽取的人数。
(3)设第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,则从六位同学中抽两位同学有15中情况,其中其中第
,则从六位同学中抽两位同学有15中情况,其中其中第![]() 组的
组的![]() 位同学为
位同学为![]() 至少有一位同学入选的有其中第
至少有一位同学入选的有其中第![]() 组的
组的![]() 位同学为
位同学为![]() 至少有一位同学入选的有9种,进而得到概率值。
至少有一位同学入选的有9种,进而得到概率值。
解:(Ⅰ)由题设可知,第![]() 组的频率为
组的频率为![]() 第
第![]() 组的频率为
组的频率为![]()
第![]() 组的频率为
组的频率为![]() 。 ……………………………………………………3分
。 ……………………………………………………3分
(Ⅱ)第![]() 组的人数为
组的人数为![]() 第
第![]() 组的人数为
组的人数为![]()
第![]() 组的人数为
组的人数为![]() 。 ……………………………………………………6分
。 ……………………………………………………6分
因为第![]() 组共有
组共有![]() 名学生,所以利用分层抽样在
名学生,所以利用分层抽样在![]() 名学生中抽取
名学生中抽取![]() 名学生,每组抽取的人数分别为: 第
名学生,每组抽取的人数分别为: 第![]() 组:
组:![]() 第
第![]() 组:
组:![]() 第
第![]() 组:
组:![]()
所以第![]() 组分别抽取
组分别抽取![]() 人、
人、![]() 人、
人、![]() 人 …………………………………………9分
人 …………………………………………9分
(Ⅲ)设第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() ,则从六位同学中抽两位同学有:
,则从六位同学中抽两位同学有:![]()
![]()
![]()
共![]() 种可能。 ……………………………………………10分
种可能。 ……………………………………………10分
其中第![]() 组的
组的![]() 位同学为
位同学为![]() 至少有一位同学入选的有:
至少有一位同学入选的有:![]()
![]() 共
共![]() 种可能, ……………………11分
种可能, ……………………11分
所以第![]() 组至少有一名学生被甲考官面试的概率为
组至少有一名学生被甲考官面试的概率为![]() …………………12分
…………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点的双曲线
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为 .
.(1)求双曲线
 的方程;
的方程;(2)若直线
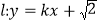 与双曲线
与双曲线 恒有两个不同的交点
恒有两个不同的交点 和
和 ,且
,且 (其中
(其中 为坐标原点),求实数
为坐标原点),求实数 取值范围.
取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,设椭圆
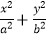 =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.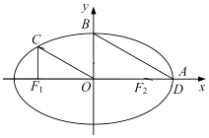
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ≤e≤
≤e≤ 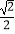 ,求
,求 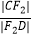 的取值范围.
的取值范围.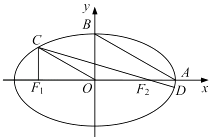
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f(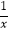 )﹣1≥
)﹣1≥ 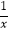 e
e  +
+ 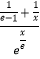 恒成立,求a的取值范围.
恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线l过定点P(1,1),且倾斜角为 ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为  .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足
满足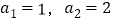 ,对每个正整数
,对每个正整数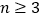 ,有
,有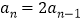 或
或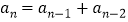 .如这个数列可以为1,2,4,6,10….
.如这个数列可以为1,2,4,6,10….(1)若某一项
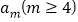 为奇数,且不为3的倍数,证明:
为奇数,且不为3的倍数,证明: ;
;(2)证明:
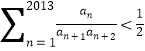 ;
;(3)若在
 的前2015项中,恰有t个项为奇数,求t的最大值.
的前2015项中,恰有t个项为奇数,求t的最大值.
相关试题

