【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
参考答案:
【答案】
(1)解:a=0时,f(x)=xe2x﹣lnx,
∴ ![]() ,
, ![]() ,
,
∴函数f′(x)在(0,+∞)上是增函数,
又函数f′(x)的值域为R,
故x0>0,使得f′(x0)=(2x0+1)e ![]() ﹣
﹣ ![]() =0,
=0,
又∵ ![]() ,∴
,∴ ![]() ,∴当x∈[
,∴当x∈[ ![]() ]时,f′(x)>0,
]时,f′(x)>0,
即函数f(x)在区间[ ![]() ,1]上递增,∴
,1]上递增,∴ ![]()
(2)解: ![]() ,
,
由(1)知函数f′(x)在(0,+∞)上是增函数,且x0>0,使得f′(x0)=0,
进而函数f(x)在区间(0,x0)上递减,在(x0,+∞)上递增,
![]() ﹣lnx0﹣ax0,
﹣lnx0﹣ax0,
由f′(x0)=0,得:(2x0+1)e ![]() ﹣
﹣ ![]() ﹣a=0,
﹣a=0,
∴ ![]() ,∴f(x0)=1﹣lnx0﹣2x02
,∴f(x0)=1﹣lnx0﹣2x02 ![]() ,
,
∵x>0,不等式f(x)≥1恒成立,
∴1﹣lnx0﹣2x02e ![]() ≥1,∴lnx0+2x02
≥1,∴lnx0+2x02 ![]() ≤0,
≤0,
设h(x0)=lnx0+2x ![]() e
e ![]() ,则h(x0)为增函数,且有唯一零点,设为t,
,则h(x0)为增函数,且有唯一零点,设为t,
则h(t)=lnt+2t2e2t=0,则﹣lnt=2t2e2t,即 ![]() ,
,
令g(x)=xex,则g(x)单调递增,且g(2t)=g( ![]() ),
),
则2t=ln ![]() ,即
,即 ![]() ,
,
∵a=(2x0+1) ![]() ﹣
﹣ ![]() 在(0,t]为增函数,
在(0,t]为增函数,
则当x0=t时,a有最大值, ![]() =
= ![]() ,
,
∴a≤2,∴a的取值范围是(﹣∞,2]
(3)解:由f( ![]() )﹣1≥
)﹣1≥ 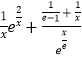 ,
,
得 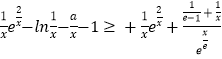 ,
,
∴xlnx﹣x﹣a≥ ![]() ,∴a
,∴a 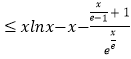 对任意x>0成立,
对任意x>0成立,
令函数g(x)=xlnx﹣x﹣ ![]() ,∴
,∴ ![]() ,
,
当x>1时,g′(x)>0,当0<x<1时,g′(x)<0,
∴当x=1时,函数g(x)取得最小值g(1)=﹣1﹣ ![]() =﹣1﹣
=﹣1﹣ ![]() ,
,
∴a≤﹣1﹣ ![]() .
.
∴a的取值范围是(﹣∞,﹣1﹣ ![]() )
)
【解析】(1)a=0时, ![]() ,
, ![]() ,由此利用导数性质能求出函数f(x)在[
,由此利用导数性质能求出函数f(x)在[ ![]() ,1]上的最小值.(2)
,1]上的最小值.(2) ![]() ,函数f(x)在区间(0,x0)上递减,在(x0 , +∞)上递增,由x>0,不等式f(x)≥1恒成立,得lnx0+2x02
,函数f(x)在区间(0,x0)上递减,在(x0 , +∞)上递增,由x>0,不等式f(x)≥1恒成立,得lnx0+2x02 ![]() ≤0,由此能求出a的取值范围.(3)由f(
≤0,由此能求出a的取值范围.(3)由f( ![]() )﹣1≥
)﹣1≥ 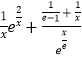 ,得a
,得a 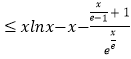 对任意x>0成立,令函数g(x)=xlnx﹣x﹣
对任意x>0成立,令函数g(x)=xlnx﹣x﹣ ![]() ,则
,则 ![]() ,由此利用导数性质能求出a的取值范围.
,由此利用导数性质能求出a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:
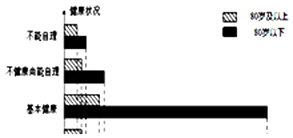
(1)若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发 放生活补贴,标准如下:①80岁及以上长者每人每月发放生活补贴200元;②80岁以下 老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100 元.试估计政府执行此计划的年度预算. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点的双曲线
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为 .
.(1)求双曲线
 的方程;
的方程;(2)若直线
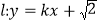 与双曲线
与双曲线 恒有两个不同的交点
恒有两个不同的交点 和
和 ,且
,且 (其中
(其中 为坐标原点),求实数
为坐标原点),求实数 取值范围.
取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,设椭圆
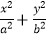 =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.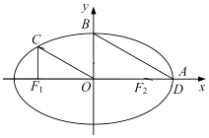
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ≤e≤
≤e≤ 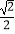 ,求
,求 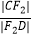 的取值范围.
的取值范围.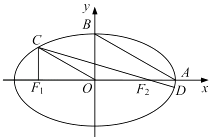
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组
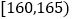 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示。
,得到的频率分布直方图如图所示。
(1)求第3、4、5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线l过定点P(1,1),且倾斜角为 ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为  .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值.
相关试题

