【题目】选修4-4:坐标系与参数方程
已知直线l过定点P(1,1),且倾斜角为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值.
参考答案:
【答案】
(1)解:∵曲线C的极坐标方程为 ![]() ,
,
∴ρ2=2ρcosθ+3,
将ρ2=x2+y2,ρcosθ=x代入,得x2+y2=2x+3,即x2+y2﹣2x﹣3=0.
∵直线l过定点P(1,1),且倾斜角为 ![]() ,
,
则直线l的参数方程为 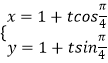 ,即
,即 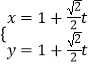 (t为参数)
(t为参数)
(2)解:将直线l的参数方程代入x2+y2﹣2x﹣3=0,得 ![]() ,
,
设方程两根分别为t1,t2,则 ![]() ,
,
∴AB的长|AB|=|t1﹣t2|= ![]() =
= ![]() =
= ![]() ,
,
|PA||PB|=|t1t2|=3
【解析】(1)曲线C的极坐标方程转为ρ2=2ρcosθ+3,将ρ2=x2+y2 , ρcosθ=x代入,能求出曲线C的直角坐标方程;由直线l过定点P(1,1),且倾斜角为 ![]() ,能求出直线l的参数方程.(2)将直线l的参数方程代入x2+y2﹣2x﹣3=0,得
,能求出直线l的参数方程.(2)将直线l的参数方程代入x2+y2﹣2x﹣3=0,得 ![]() ,设方程两根分别为t1 , t2 , 利用韦达定理及弦长公式能求出|AB|及|PA||PB|的值.
,设方程两根分别为t1 , t2 , 利用韦达定理及弦长公式能求出|AB|及|PA||PB|的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,设椭圆
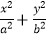 =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.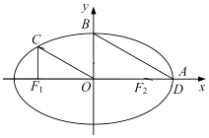
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ≤e≤
≤e≤ 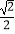 ,求
,求 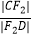 的取值范围.
的取值范围.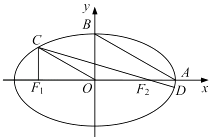
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f(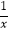 )﹣1≥
)﹣1≥ 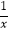 e
e  +
+ 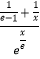 恒成立,求a的取值范围.
恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组
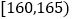 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示。
,得到的频率分布直方图如图所示。
(1)求第3、4、5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足
满足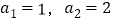 ,对每个正整数
,对每个正整数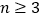 ,有
,有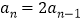 或
或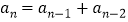 .如这个数列可以为1,2,4,6,10….
.如这个数列可以为1,2,4,6,10….(1)若某一项
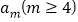 为奇数,且不为3的倍数,证明:
为奇数,且不为3的倍数,证明: ;
;(2)证明:
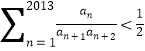 ;
;(3)若在
 的前2015项中,恰有t个项为奇数,求t的最大值.
的前2015项中,恰有t个项为奇数,求t的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列有关命题的说法正确的是( )
A.命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0”
B.“若x+y=0,则x,y互为相反数”的逆命题为真命题
C.命题“x∈R,使得2x2﹣1<0”的否定是:“x∈R,均有2x2﹣1<0”
D.命题“若cosx=cosy,则x=y”的逆否命题为真命题
相关试题

