【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2 ![]() ,PA=2,求:
,PA=2,求: 
(1)三角形PCD的面积;
(2)异面直线BC与AE所成的角的大小.
参考答案:
【答案】
(1)解:∵PA⊥底面ABCD,CD底面ABCD,
∴CD⊥PA.
∵矩形ABCD中,CD⊥AD,而PA、AD是平面PAD的交线.
∴CD⊥平面PDA,
∵PD平面PDA,∴CD⊥PD,三角形PCD是以D为直角顶点的直角三角形.
∵Rt△PAD中,AD=2 ![]() ,PA=2,
,PA=2,
∴PD= ![]() =2
=2 ![]() .
.
∴三角形PCD的面积S= ![]() ×PD×DC=2
×PD×DC=2 ![]() .
.
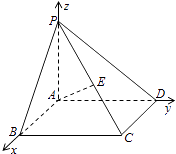
(2)解:[解法一]
如图所示,建立空间直角坐标系,可得B(2,0,0),C(2,2 ![]() ,0),E(1,
,0),E(1, ![]() ,1).
,1).
∴ ![]() =(1,
=(1, ![]() ,1),
,1), ![]() =(0,2
=(0,2 ![]() ,0),
,0),
设 ![]() 与
与 ![]() 夹角为θ,则cosθ=
夹角为θ,则cosθ= 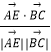 =
= ![]() =
= ![]() ,
,
∴θ= ![]() ,由此可得异面直线BC与AE所成的角的大小为
,由此可得异面直线BC与AE所成的角的大小为 ![]() .
.
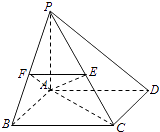
[解法二]
取PB的中点F,连接AF、EF、AC,
∵△PBC中,E、F分别是PC、PB的中点,
∴EF∥BC,∠AEF或其补角就是异面直线BC与AE所成的角.
∵Rt△PAC中,PC= ![]() =4.
=4.
∴AE= ![]() PC=2,
PC=2,
∵在△AEF中,EF= ![]() BC=
BC= ![]() ,AF=
,AF= ![]() PB=
PB= ![]()
∴AF2+EF2=AE2,△AEF是以F为直角顶点的等腰直角三角形,
∴∠AEF= ![]() ,可得异面直线BC与AE所成的角的大小为
,可得异面直线BC与AE所成的角的大小为 ![]() .
.
【解析】(1)可以利用线面垂直的判定与性质,证明出三角形PCD是以D为直角顶点的直角三角形,然后在Rt△PAD中,利用勾股定理得到PD=2 ![]() ,最后得到三角形PCD的面积S;(2)[解法一]建立如图空间直角坐标系,可得B、C、E各点的坐标,从而
,最后得到三角形PCD的面积S;(2)[解法一]建立如图空间直角坐标系,可得B、C、E各点的坐标,从而 ![]() =(1,
=(1, ![]() ,1),
,1), ![]() =(0,2
=(0,2 ![]() ,0),利用空间向量数量积的公式,得到
,0),利用空间向量数量积的公式,得到 ![]() 与
与 ![]() 夹角θ满足:cosθ=
夹角θ满足:cosθ= ![]() ,由此可得异面直线BC与AE所成的角的大小为
,由此可得异面直线BC与AE所成的角的大小为 ![]() ;[解法二]取PB的中点F,连接AF、EF,△PBC中,利用中位线定理,得到EF∥BC,从而∠AEF或其补角就是异面直线BC与AE所成的角,然后可以通过计算证明出:△AEF是以F为直角顶点的等腰直角三角形,所以∠AEF=
;[解法二]取PB的中点F,连接AF、EF,△PBC中,利用中位线定理,得到EF∥BC,从而∠AEF或其补角就是异面直线BC与AE所成的角,然后可以通过计算证明出:△AEF是以F为直角顶点的等腰直角三角形,所以∠AEF= ![]() ,可得异面直线BC与AE所成的角的大小为
,可得异面直线BC与AE所成的角的大小为 ![]() .
.
【考点精析】本题主要考查了异面直线及其所成的角和直线与平面垂直的性质的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;垂直于同一个平面的两条直线平行才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
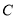 与圆
与圆 :
: 关于直线
关于直线 对称.
对称.(1)求圆
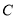 的标准方程;
的标准方程;(2)已知点
 ,若与直线
,若与直线 垂直的直线
垂直的直线 与圆
与圆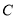 交于不同两点
交于不同两点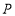 、
、 ,且
,且 是钝角,求直线
是钝角,求直线 在
在 轴上的截距的取值范围.
轴上的截距的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
 的函数
的函数 在
在 上有最大值1,设
上有最大值1,设 .
.(1)求
 的值;
的值;(2)若不等式
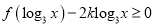 在
在 上恒成立,求实数
上恒成立,求实数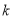 的取值范围;
的取值范围;(3)若函数
 有三个不同的零点,求实数
有三个不同的零点,求实数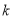 的取值范围(
的取值范围( 为自然对数的底数).
为自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=lg(x+1)
(1)若0<f(1﹣2x)﹣f(x)<1,求x的取值范围;
(2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,g(x)=f(x),求函数y=g(x)(x∈[1,2])的反函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里A处,如图,现假设:

①失事船的移动路径可视为抛物线 ;
;
②定位后救援船即刻沿直线匀速前往救援;
③救援船出发t小时后,失事船所在位置的横坐标为7t
(1)当t=0.5时,写出失事船所在位置P的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向.
(2)问救援船的时速至少是多少海里才能追上失事船? -
科目: 来源: 题型:
查看答案和解析>>【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,如图是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成
 列联表,并据此资料你是否有
列联表,并据此资料你是否有 的把握认为选手成绩“优秀”与文化程度有关?
的把握认为选手成绩“优秀”与文化程度有关?
注:
 ,其中
,其中 .
.
(2)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
(3)如果在优秀等级的选手中取4名,在良好等级的选手中取2名,再从这6人中任选3人组成一个比赛团队,求所选团队中有2名选手的等级为优秀的概率.
相关试题

