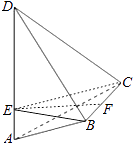
【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 . 
参考答案:
【答案】![]()
【解析】解:作BE⊥AD于E,连接CE,则AD⊥平面BEC,所以CE⊥AD,
由题设,B与C都是在以AD为焦点的椭球上,且BE、CE都垂直于焦距AD,
AB+BD=AC+CD=2a,显然△ABD≌△ACD,所以BE=CE.
取BC中点F,∴EF⊥BC,EF⊥AD,要求四面体ABCD的体积的最大值,因为AD是定值,只需三角形EBC的面积最大,因为BC是定值,所以只需EF最大即可,
当△ABD是等腰直角三角形时几何体的体积最大,∵AB+BD=AC+CD=2a,
∴AB=a,所以EB= ![]() ,EF=
,EF= ![]() ,
,
所以几何体的体积为: ![]() ×
× ![]() =
= ![]() .
.
所以答案是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a为正实数,n为自然数,抛物线
 与x轴正半轴相交于点A,设f(n)为该抛物线在点A处的切线在y轴上的截距.
与x轴正半轴相交于点A,设f(n)为该抛物线在点A处的切线在y轴上的截距.
(1)用a和n表示f(n);
(2)求对所有n都有 成立的a的最小值;
成立的a的最小值;
(3)当0<a<1时,比较 与
与  的大小,并说明理由.
的大小,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设10≤x1<x2<x3<x4≤104 , x5=105 , 随机变量ξ1取值x1、x2、x3、x4、x5的概率均为0.2,随机变量ξ2取值
 、
、  、
、  、
、  、
、  的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
A.Dξ1>Dξ2
B.Dξ1=Dξ2
C.Dξ1<Dξ2
D.Dξ1与Dξ2的大小关系与x1、x2、x3、x4的取值有关 -
科目: 来源: 题型:
查看答案和解析>>【题目】设an=
 sin
sin  ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 与圆
与圆 :
: 关于直线
关于直线 对称.
对称.(1)求圆
 的标准方程;
的标准方程;(2)已知点
 ,若与直线
,若与直线 垂直的直线
垂直的直线 与圆
与圆 交于不同两点
交于不同两点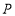 、
、 ,且
,且 是钝角,求直线
是钝角,求直线 在
在 轴上的截距的取值范围.
轴上的截距的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
 的函数
的函数 在
在 上有最大值1,设
上有最大值1,设 .
.(1)求
 的值;
的值;(2)若不等式
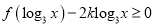 在
在 上恒成立,求实数
上恒成立,求实数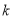 的取值范围;
的取值范围;(3)若函数
 有三个不同的零点,求实数
有三个不同的零点,求实数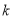 的取值范围(
的取值范围( 为自然对数的底数).
为自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
 ,PA=2,求:
,PA=2,求: 
(1)三角形PCD的面积;
(2)异面直线BC与AE所成的角的大小.
相关试题

