【题目】已知定义域为![]() 的函数
的函数![]() 在
在![]() 上有最大值1,设
上有最大值1,设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 有三个不同的零点,求实数
有三个不同的零点,求实数![]() 的取值范围(
的取值范围(![]() 为自然对数的底数).
为自然对数的底数).
参考答案:
【答案】(1)0;(2)![]() ;(3)
;(3)![]()
![]()
【解析】
(1)结合二次函数的性质 可判断g(x)在[1,2]上的单调性,结合已知函数的最大值可求m;(2)由(1)可知f(x),由原不等式可知2k![]() 1在x∈[3,9]上恒成立,结合对数与二次函数的性质可求;(3)原方程可化为|ex﹣1|2﹣(3k+2)|ex﹣1|+(2k+1)=0,利用换元q=|ex﹣1|,结合二次函数的 实根分布即可求解.
1在x∈[3,9]上恒成立,结合对数与二次函数的性质可求;(3)原方程可化为|ex﹣1|2﹣(3k+2)|ex﹣1|+(2k+1)=0,利用换元q=|ex﹣1|,结合二次函数的 实根分布即可求解.
(1)因为![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,解得
,解得![]() .
.
(2)由(1)可得:![]()
所以不等式![]() 在
在![]() 上恒成立.
上恒成立.
等价于![]() 在
在![]() 上恒成立
上恒成立
令![]() ,因为
,因为![]() ,所以
,所以![]()
则有![]() 在
在![]() 恒成立
恒成立
令![]() ,
,![]() ,则
,则![]()
所以![]() ,即
,即![]() ,所以实数
,所以实数![]() 的取值范围为
的取值范围为![]() .
.
(3)因为![]()
令![]() ,由题意可知
,由题意可知![]()
令![]() ,
,![]()
则函数![]() 有三个不同的零点
有三个不同的零点
等价于![]() 在
在![]() 有两个零点,
有两个零点,
当![]() ,此时方程
,此时方程![]() ,此时关于
,此时关于![]() 方程有三个零点,符合题意;
方程有三个零点,符合题意;
当![]() 记为
记为![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]()
所以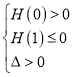 ,解得
,解得![]()
综上实数![]() 的取值范围
的取值范围![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设an=
 sin
sin  ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
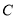 与圆
与圆 :
: 关于直线
关于直线 对称.
对称.(1)求圆
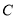 的标准方程;
的标准方程;(2)已知点
 ,若与直线
,若与直线 垂直的直线
垂直的直线 与圆
与圆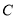 交于不同两点
交于不同两点 、
、 ,且
,且 是钝角,求直线
是钝角,求直线 在
在 轴上的截距的取值范围.
轴上的截距的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
 ,PA=2,求:
,PA=2,求: 
(1)三角形PCD的面积;
(2)异面直线BC与AE所成的角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=lg(x+1)
(1)若0<f(1﹣2x)﹣f(x)<1,求x的取值范围;
(2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,g(x)=f(x),求函数y=g(x)(x∈[1,2])的反函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里A处,如图,现假设:

①失事船的移动路径可视为抛物线 ;
;
②定位后救援船即刻沿直线匀速前往救援;
③救援船出发t小时后,失事船所在位置的横坐标为7t
(1)当t=0.5时,写出失事船所在位置P的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向.
(2)问救援船的时速至少是多少海里才能追上失事船?
相关试题

