【题目】参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题: 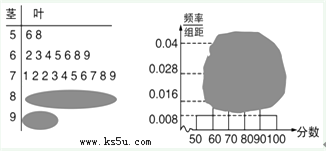
(1)求参加数学抽测的人数n、抽测成绩的中位数及分数分别在[80,90),[90,100]内的人数;
(2)若从分数在[80,100]内的学生中任选两人进行调研谈话,求恰好有一人分数在[90,100]内的概率.
参考答案:
【答案】
(1)解:分数在[50,60)内的频数为2,由频率分布直方图可以看出,分数在[90,100]内同样有2人.
由 ![]() ,得n=25,
,得n=25,
茎叶图可知抽测成绩的中位数为73.
分数在[80,90)之间的人数为25﹣(2+7+10+2)=4
参加数学竞赛人数n=25,中位数为73,分数在[80,90)、[90,100]内的人数分别为4人、2人.
(2)解:设“在[80,100]内的学生中任选两人,恰好有一人分数在[90,100]内”为事件M,
将[80,90)内的4人编号为a,b,c,d;[90,100]内的2人编号为A,B
在[80,100]内的任取两人的基本事件为:ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,cB,dA,dB,AB共15个
其中,恰好有一人分数在[90,100]内的基本事件有aA,aB,bA,bB,cA,cB,dA,dB,共8个
故所求的概率得 ![]()
答:恰好有一人分数在[90,100]内的概率为 ![]()
【解析】(1)由频率分布直方图可以看出,分数在[90,100]内同样有2人.即可得到抽测的人数n,算出分数在[80,90)之间的人数.(2)由题意知本题是一个古典概型,试验包含的所有事件可以通过列举得到结果数,看出满足条件的事件数,根据古典概型公式得到结果.
【考点精析】关于本题考查的频率分布直方图,需要了解频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟)
广告播放时长(分钟)
收视人次(万)
甲
70
5
60
乙
60
5
25
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用
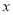 ,
,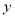 表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.(1)用
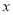 ,
,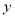 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
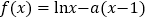
(1)求函数
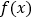 的极值;
的极值;(2)当
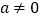 时,过原点分别做曲线
时,过原点分别做曲线 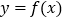 与
与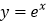 的切线
的切线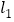 ,
,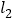 ,若两切线的斜率互为倒数,求证:
,若两切线的斜率互为倒数,求证: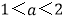 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 ,且椭圆上任意一点到左焦点的最大距离为
,且椭圆上任意一点到左焦点的最大距离为 ,最小距离为
,最小距离为 .
.(1)求椭圆的方程;
(2)过点
 的动直线
的动直线 交椭圆
交椭圆 于
于 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得以线段
,使得以线段 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求出点
?若存在,求出点 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体
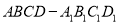 中,
中, 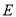 是棱
是棱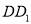 的中点.
的中点.(
 )求直线
)求直线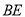 和平面
和平面 所成角的正弦值.
所成角的正弦值.(
 )在棱
)在棱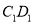 上是否存在一点
上是否存在一点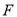 ,使
,使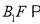 平面
平面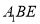 ?证明你的结论.
?证明你的结论.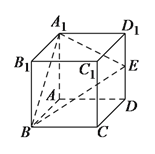
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.
(1)若用分层抽样的方法从“优秀警员”和“优秀陪练员”中共提取10人,然后再从这10人中选4人,那么至少有1人是“优秀警员”的概率是多少?
(2)若所有“优秀警员”中选3名代表,用
 表示所选女“优秀警员”的人数,试求
表示所选女“优秀警员”的人数,试求 的分布列和数学期望.
的分布列和数学期望.
相关试题

