【题目】某课题组对春晚参加“咻一咻”抢红包活动的同学进行调查,按照使用手机系统不同(安卓系统和IOS系统)分别随机抽取5名同学进行问卷调查,发现他们咻得红包总金额数如表所示:
手机系统 | 一 | 二 | 三 | 四 | 五 |
安卓系统(元) | 2 | 5 | 3 | 20 | 9 |
IOS系统(元) | 4 | 3 | 18 | 9 | 7 |
(1)如果认为“咻”得红包总金额超过6元为“咻得多”,否则为“咻得少”,请判断手机系统与咻得红包总金额的多少是否有关?
(2)要从5名使用安卓系统的同学中随机选出2名参加一项活动,以X表示选中的同学中咻得红包总金额超过6元的人数,求随机变量X的分布列及数学期望E(X).
下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
独立性检验统计量 ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考答案:
【答案】
(1)解:根据题意列出2×2列联表如下:
咻得多少 手机系统 | 咻得多 | 咻得少 | 合计 |
安卓 | 3 | 2 | 5 |
IOS | 2 | 3 | 5 |
合计 | 5 | 5 | 10 |
K2= ![]() =0.4<2.706,
=0.4<2.706,
所以没有足够的理由认为手机系统与咻得红包总金额的多少有关
(2)解:随机变量X的所有可能取值为0,1,2,
P(X=0)= ![]() =
= ![]() ;
;
P(X=1)= ![]() =
= ![]() ;
;
P(X=2)= ![]() =
= ![]()
故X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
∴数学期望E(X),E(X)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =0.8
=0.8
【解析】(1)根据题意列出2×2列联表,根据2×2列联表,代入求临界值的公式,求出观测值,利用观测值同临界值表进行比较,K2=0.4<2.706,可得到没有足够的理由认为手机系统与咻得红包总金额的多少有关;(2)由题意求得X的取值0,1,2,运用排列组合的知识,可得各自的概率,求得X的分布列,由期望公式计算即可得到(X).;
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设全集为R,函数
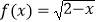 的定义域为M,则RM为( )
的定义域为M,则RM为( )
A.(2,+∞)
B.(﹣∞,2)
C.(﹣∞,2]
D.[2,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x),g(x)都是定义在R上的函数,并满足:
1)f(x)=2axg(x),(a>0,a≠1);
2)g(x)≠0;
3)f(x)g′(x)<f′(x)g(x)且 +
+  =5,则a= .
=5,则a= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在△ABC内,AB=CP=2,BC=3,∠P+∠B=π,记∠B=α.
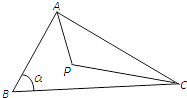
(1)试用α表示AP的长;
(2)求四边形ABCP的面积的最大值,并写出此时α的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=log
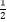 (x2﹣2x)的单调递增区间是( )
(x2﹣2x)的单调递增区间是( )
A.(1,+∞)
B.(2,+∞)
C.(﹣∞,0)
D.(﹣∞,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50 名,其中每天玩微信超过6 小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控
非微信控
合计
男性
26
24
50
女性
30
20
50
合计
56
44
100
(1)根据以上数据,能否有60%的把握认为“微信控”与”性别“有关?
(2)现从调查的女性用户中按分层抽样的方法选出5 人并从选出的5 人中再随机抽取3 人赠送200 元的护肤品套装,记这3 人中“微信控”的人数为X,试求X 的分布列与数学期望.
参考公式:
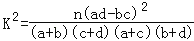 ,其中n=a+b+c+d.
,其中n=a+b+c+d. P(K2≥k0)
0.50
0.40
0.25
0.05
0.025
0.010
k0
0.455
0.708
1.323
3.841
5.024
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺.大鼠日自倍,小鼠日自半.问几何日相逢?各穿几何?”,翻译成今天的话是:一只大鼠和一只小鼠分别从的墙两侧面对面打洞,已知第一天两鼠都打了一尺长的洞,以后大鼠每天打的洞长是前一天的2倍,小鼠每天打的洞长是前一天的一半,已知墙厚五尺,问两鼠几天后相见?相见时各打了几尺长的洞?设两鼠x 天后相遇(假设两鼠每天的速度是匀速的),则x=( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

