【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,
, ![]() 是平面上一点,若存在过点
是平面上一点,若存在过点![]() 的直线与
的直线与![]() 都有公共点,则称
都有公共点,则称![]() 为“
为“![]() 型点”.
型点”.

(1)证明: ![]() 的左焦点是“
的左焦点是“![]() 型点”;
型点”;
(2)设直线![]() 与
与![]() 有公共点,求证:
有公共点,求证: ![]() ,进而证明原点不是“
,进而证明原点不是“![]() 型点”;
型点”;
(3)求证: ![]() 内的点都不是“
内的点都不是“![]() 型点”.
型点”.
参考答案:
【答案】(1) ![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)由题意![]() 的左焦点为
的左焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 、
、![]() 交于
交于![]() ,即可判定,得出直线方程;
,即可判定,得出直线方程;
(2)联立方程组![]() 和
和![]() ,根据方程有解,即可求解
,根据方程有解,即可求解![]() 的范围,从而判断原点不是“
的范围,从而判断原点不是“![]() 型点”;
型点”;
(3)以![]() 为边界的正方形区域记为
为边界的正方形区域记为![]() ,分点
,分点![]() 在
在![]() 的边界上,和
的边界上,和![]() 是区域
是区域![]() 内的点,两种情况分类讨论,进而说明
内的点,两种情况分类讨论,进而说明![]() ,联立方程组,得出
,联立方程组,得出![]() ,得出直线与曲线没有公共点,从而证得结论.
,得出直线与曲线没有公共点,从而证得结论.
试题解析:
(1)![]() 的左焦点为
的左焦点为![]() ,
,
过![]() 的直线
的直线![]() 与
与![]() 交于
交于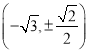 ,与
,与![]() 交于
交于![]() ,故
,故![]() 的左焦点为“
的左焦点为“![]() 型点”,且直线可以为
型点”,且直线可以为![]() ;
;
(2)直线![]() 与
与![]() 有交点,则
有交点,则![]() ,
,
若方程组有解,则必须![]() ;
;
直线![]() 与
与![]() 有交点,则
有交点,则![]() ,
,
若方程组有解,则必须![]()
故直线![]() 至多与曲线
至多与曲线![]() 和
和![]() 中的一条有交点,即原点不是“
中的一条有交点,即原点不是“![]() 型点”
型点”
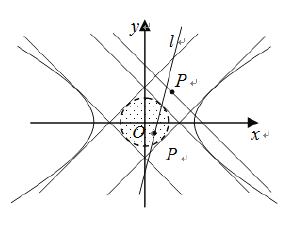
(3)以![]() 为边界的正方形区域记为
为边界的正方形区域记为![]() .
.
1)若点![]() 在
在![]() 的边界上,则该边所在直线与
的边界上,则该边所在直线与![]() 相切,与
相切,与![]() 有公共部分,即
有公共部分,即![]() 边界上的点都是“
边界上的点都是“![]() 型点”;
型点”;
2)设![]() 是区域
是区域![]() 内的点,即
内的点,即![]() ,
,
假设![]() 是“
是“![]() 型点”,则存在过点
型点”,则存在过点![]() 的直线
的直线![]() 与
与![]() 都有公共点.
都有公共点.
ⅰ)若直线![]() 与
与![]() 有公共点,直线
有公共点,直线![]() 的方程化为
的方程化为![]() ,假设
,假设![]() ,则
,则![]() ,
,
可知直线![]() 在
在![]() 之间,与
之间,与![]() 无公共点,这与“直线
无公共点,这与“直线![]() 与
与![]() 有公共点”矛盾,所以得到:与
有公共点”矛盾,所以得到:与![]() 有公共点的直线
有公共点的直线![]() 的斜率
的斜率![]() 满足
满足![]() .
.
ⅱ)假设![]() 与
与![]() 也有公共点,则方程组
也有公共点,则方程组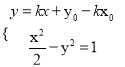 有实数解.
有实数解.
从方程组得![]() ,
,
![]() ,由
,由![]() ,
, ![]()
因为![]()
![]()
所以, ![]() ,即直线
,即直线![]() 与
与![]() 没有公共点,与“直线
没有公共点,与“直线![]() 与
与![]() 有公共点”矛盾,于是可知
有公共点”矛盾,于是可知![]() 不是“
不是“![]() 型点”.
型点”.
证明完毕
另解: ![]()
令![]() ,因为
,因为![]() ,所以|
,所以|![]() ,即
,即![]() .于是可知
.于是可知![]() 的图像是开口向下的抛物线,且对称轴方程为是
的图像是开口向下的抛物线,且对称轴方程为是![]() ,因为
,因为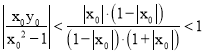 ,
,
所以![]() 在区间
在区间![]() 上为增函数,在
上为增函数,在![]() 上为减函数.
上为减函数.
因为![]() ,
, ![]() ,所以对任意
,所以对任意![]() ,都有
,都有![]() ,即直线
,即直线![]() 与
与![]() 没有公共点,与“直线
没有公共点,与“直线![]() 与
与![]() 有公共点”矛盾,于是可知
有公共点”矛盾,于是可知![]() 不是“
不是“![]() 型点”.
型点”.
证明完毕.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示.
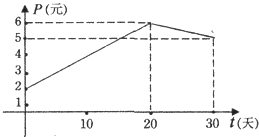
第t天
4
10
16
22
Q(万股)
36
30
24
18
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.若二面角B1﹣DC﹣C1的大小为60°,则AD的长为( )

A.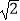
B.
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|a﹣1≤x≤a+1},集合B={x|﹣1≤x≤5}.
(1)若a=5,求A∩B;
(2)若A∪B=B,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)(x∈R)是偶函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式;
(2)若不等式f(x)≥mx在1≤x≤2时都成立,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知销售“笔记本电脑”和“台式电脑”所得的利润分别是P(单位:万元)和Q(单位:万元),它们与进货资金t(单位:万元)的关系有经验公式P=
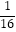 t和Q=
t和Q= 
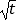 .某商场决定投入进货资金50万元,全部用来购入这两种电脑,那么该商场应如何分配进货资金,才能使销售电脑获得的利润y(单位:万元)最大?最大利润是多少万元?
.某商场决定投入进货资金50万元,全部用来购入这两种电脑,那么该商场应如何分配进货资金,才能使销售电脑获得的利润y(单位:万元)最大?最大利润是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】设F1 , F为椭圆C1:
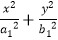 =1,(a1>b1>0)与双曲线C2的公共左、右焦点,它们在第一象限内交于点M,△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2,若椭圆C1的离心率e∈[
=1,(a1>b1>0)与双曲线C2的公共左、右焦点,它们在第一象限内交于点M,△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2,若椭圆C1的离心率e∈[  ,
,  ],则双曲线C2的离心率的取值范围是( )
],则双曲线C2的离心率的取值范围是( )
A.[ ,
,  ]
]
B.[ ,++∞)
,++∞)
C.(1,4]
D.[ ,4]
,4]
相关试题

