搜索
【题目】如图，在直三棱柱ABC﹣A1B1C1中，∠ACB=90°，2AC=AA1=BC=2．若二面角B1﹣DC﹣C1的大小为60°，则AD的长为（ ） 
A.
B.
C.2
D.
参考答案：
【答案】A
【解析】解：∵∠A1C1B1=∠ACB=90°，∴B1C1⊥A1C1 ，
又由直三棱柱性质知B1C1⊥CC1 ，
∴B1C1⊥平面ACC1A1 ．
如图，在面ACC1A1内过C1作C1E⊥CD，交CD或延长线或于E，连EB1 ，
由三垂线定理可知∠B1EC1为二面角B1﹣DC﹣C1的平面角，
∴∠B1EC1=60°．
由B1C1=2知，C1E= 
设AD=x，则DC= 
．
∵△DCC1的面积为1，
∴ 
． ． =1，
解得x= 
即AD=
故选A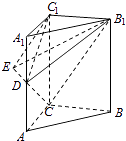
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，椭圆M：
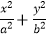=1（a＞b＞0）的离心率为 
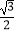，直线x=±a和y=±b所围成的矩形ABCD的面积为8．
（Ⅰ）求椭圆M的标准方程；
（Ⅱ）设直线l：y=x+m（m∈R）与椭圆M有两个不同的交点P，Q，l与矩形ABCD有两个不同的交点S，T．求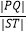
的最大值及取得最大值时m的值．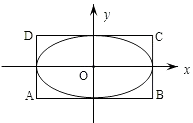
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义在（﹣1，1）上的函数f（x）满足：f（x）﹣f（y）=f（
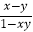），当x∈（﹣1，0）时，有f（x）＞0；若P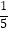=f（ 
）+f（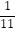 
），Q=f（ 
），R=f（0）；则P，Q，R的大小关系为 ． -
科目： 来源： 题型：
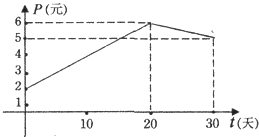
查看答案和解析>>【题目】某上市股票在30天内每股的交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在下图中的两条线段上，该股票在30天内（包括30天）的日交易量Q（万股）与时间t（天）的部分数据如下表所示．
第t天
4
10
16
22
Q（万股）
36
30
24
18
（1）根据提供的图象，写出该种股票每股交易价格P（元）与时间t（天）所满足的函数关系式；
（2）根据表中数据确定日交易量Q（万股）与时间t（天）的一次函数关系式；
（3）在（2）的结论下，用y（万元）表示该股票日交易额，写出y关于t的函数关系式，并求出这30天中第几日交易额最大，最大值为多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】设集合A={x|a﹣1≤x≤a+1}，集合B={x|﹣1≤x≤5}．
（1）若a=5，求A∩B；
（2）若A∪B=B，求实数a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知曲线
，曲线
， 
是平面上一点，若存在过点
的直线与
都有公共点，则称
为“
型点”.
（1）证明：
的左焦点是“
型点”；（2）设直线
与
有公共点，求证： 
，进而证明原点不是“
型点”；（3）求证：
内的点都不是“
型点”. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知y=f（x）（x∈R）是偶函数，当x≥0时，f（x）=x2﹣2x．
（1）求f（x）的解析式；
（2）若不等式f（x）≥mx在1≤x≤2时都成立，求m的取值范围．
相关试题
