【题目】如图,已知等腰直角三角形![]() 的斜边
的斜边![]() 所在直线方程为
所在直线方程为![]() ,其中
,其中![]() 点在
点在![]() 点上方,直角顶点
点上方,直角顶点![]() 的坐标为
的坐标为![]() .
.

(1)求![]() 边上的高线
边上的高线![]() 所在直线的方程;
所在直线的方程;
(2)求等腰直角三角形![]() 的外接圆的标准方程;
的外接圆的标准方程;
(3)分别求两直角边![]() ,
,![]() 所在直线的方程.
所在直线的方程.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)利用垂直斜率相乘为-1得到CH斜率,点斜式得到CH方程.
(2)首先计算圆心,再计算半径,得到圆的标准方程.
(3)设直线AC方程,通过H到直线的距离计算得到AC,BC直线.
(1)因为等腰直角三角形![]() 的斜边
的斜边![]() 所在直线方程为
所在直线方程为![]() ,设
,设![]() 的斜率为
的斜率为![]()
则![]()
![]() 经过点
经过点![]() ,所以
,所以![]()
(2)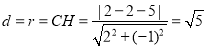
![]() 解得:
解得:![]() ,所以圆心
,所以圆心![]()
所以等腰直角三角形![]() 的外接圆的标准方程为
的外接圆的标准方程为![]()
(3)经判断,![]() 斜率均存在
斜率均存在
设![]() ,即
,即![]() ,因为
,因为![]() 到直线
到直线![]() 的距离为
的距离为![]()
所以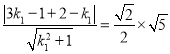
解得:![]() 或
或![]()
因为![]() 点在
点在![]() 点上方,所以
点上方,所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占
 .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)求出
 的值;
的值;(2)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某理科考生参加自主招生面试,从
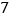 道题中(
道题中(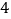 道甲组题和
道甲组题和 道乙组题)不放回地依次任取
道乙组题)不放回地依次任取 道作答.
道作答.(1)求该考生在第一次抽到甲组题的条件下,第二次和第三次均抽到乙组题的概率;
(2)规定理科考生需作答
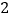 道甲组题和
道甲组题和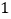 道乙组题,该考生答对甲组题的概率均为
道乙组题,该考生答对甲组题的概率均为 ,答对乙组题的概率均为
,答对乙组题的概率均为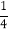 ,若每题答对得
,若每题答对得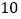 ,否则得零分.现该生已抽到
,否则得零分.现该生已抽到 道题(
道题(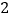 道甲组题和
道甲组题和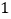 道乙组题),求其所得总分的分布列与数学期望.
道乙组题),求其所得总分的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2|x+1|+|2x﹣a|(x∈R).
(1)当a>﹣2时,函数f(x)的最小值为4,求实数a的值;
(2)若对于任意,x∈[﹣1,4],不等式f(x)≥3x恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,平面
中,平面 平面
平面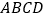 ,
,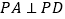 ,
, ,
, ,
, ,
, ,
, .
.
(1)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.(2)在棱
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四面体
 中,平面
中,平面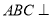 平面
平面 ,
, ,
, ,
, 分别为
分别为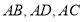 的中点.
的中点.
(1)证明:平面
 平面
平面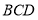 ;
;(2)求三棱锥
 的体积;
的体积;(3)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生对数学学案质量的满意度,从高一、高二两个年级分别随机调查了20个学生,得到对学案满意度评分(满分100分)的茎叶图如图:则下列说法错误的是( )

A.高一学生满意度评分的平均值比高二学生满意度评分的平均值高
B.高一学生满意度评分比较集中,高二学生满意度评分比较分散
C.高一学生满意度评分的中位数为80
D.高二学生满意度评分的中位数为74
相关试题

