【题目】某校为了解学生对数学学案质量的满意度,从高一、高二两个年级分别随机调查了20个学生,得到对学案满意度评分(满分100分)的茎叶图如图:则下列说法错误的是( ) 
A.高一学生满意度评分的平均值比高二学生满意度评分的平均值高
B.高一学生满意度评分比较集中,高二学生满意度评分比较分散
C.高一学生满意度评分的中位数为80
D.高二学生满意度评分的中位数为74
参考答案:
【答案】D
【解析】解:由茎叶图可得.高二学生满意度评分的中位数为 ![]() ,所以D错误. 故选:D
,所以D错误. 故选:D
【考点精析】认真审题,首先需要了解茎叶图(茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰直角三角形
 的斜边
的斜边 所在直线方程为
所在直线方程为 ,其中
,其中 点在
点在 点上方,直角顶点
点上方,直角顶点 的坐标为
的坐标为 .
.
(1)求
 边上的高线
边上的高线 所在直线的方程;
所在直线的方程;(2)求等腰直角三角形
 的外接圆的标准方程;
的外接圆的标准方程;(3)分别求两直角边
 ,
, 所在直线的方程.
所在直线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,平面
中,平面 平面
平面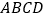 ,
,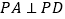 ,
, ,
, ,
, ,
, ,
, .
.
(1)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.(2)在棱
 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四面体
 中,平面
中,平面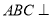 平面
平面 ,
, ,
, ,
, 分别为
分别为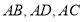 的中点.
的中点.
(1)证明:平面
 平面
平面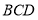 ;
;(2)求三棱锥
 的体积;
的体积;(3)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=sin(ωx+φ)+
 的图象过(1,2),若f(x)相邻的零点为x1 , x2且满足|x1﹣x2|=6,则f(x)的单调增区间为( )
的图象过(1,2),若f(x)相邻的零点为x1 , x2且满足|x1﹣x2|=6,则f(x)的单调增区间为( )
A.[﹣2+12k,4+12k](k∈Z)
B.[﹣5+12k,1+12k](k∈Z)
C.[1+12k,7+12k](k∈Z)
D.[﹣2+6k,1+6k](k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)对任意的x∈R,都有f(﹣x)+f(x)=﹣6,且当x≥0时,f(x)=2x﹣4,定义在R上的函数g(x)=a(x﹣a)(x+a+1),两函数同时满足:x∈R,都有f(x)<0或g(x)<0;x∈(﹣∞,﹣1),f(x)g(x)<0,则实数a的取值范围为( )
A.(﹣3,0)
B.
C.(﹣3,﹣1)
D.(﹣3,﹣1] -
科目: 来源: 题型:
查看答案和解析>>【题目】在钝角△ABC中,角A,B,C所对的边分别为a,b,c且b=atanB. (Ⅰ)求A﹣B的值;
(Ⅱ)求cos2B﹣sinA的取值范围.
相关试题

