【题目】(1)对于任意实数x,不等式sin x+cos x>m恒成立,求实数m的取值范围;
(2)存在实数x,不等式sin x+cos x>m有解,求实数m的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)不等式恒成立问题,一般转化为对应函数最值问题,即sin x+cos x最小值大于m,根据函数最值可得实数m的取值范围;(2)不等式有解问题,一般转化为对应函数最值问题,即sin x+cos x最大值大于m,根据函数最值可得实数m的取值范围.
试题解析:解:(1)令y=sin x+cos x,x∈R.
∵y=sin x+cos x=![]() sin(x+
sin(x+![]() )≥-
)≥-![]() .
.
又∵x∈R,sin x+cos x>m恒成立.
∴只要m<-![]() 即可.
即可.
∴所求m的取值范围是(-∞,-![]() ).
).
(1)令y=sin x+cos x,x∈R.
∵y=sin x+cos x=![]() sin(x+
sin(x+![]() )∈[-
)∈[-![]() ,
,![]() ],
],
又∵x∈R,sin x+cos x>m有解.
∴只要m<![]() 即可.
即可.
∴所求m的取值范围是(-∞,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列命题是全称命题还是存在性命题,并判断其真假:
(1)对任意x∈R,zx>0(z>0);
(2)对任意非零实数x1,x2,若x1<x2,则
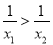 ;
;(3)α∈R,使得sin(α+
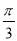 )=sin α;
)=sin α;(4)x∈R,使得x2+1=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )
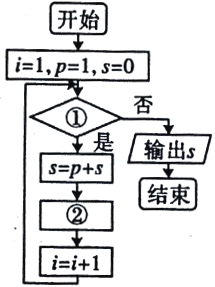
A.
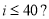 ;
; 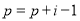 B.
B. 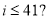 ;
; 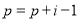
C.
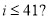 ;
; 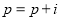 D.
D. 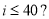 ;
; 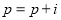
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
 .
.(Ⅰ)求
 的最小值及取得最小值时
的最小值及取得最小值时 的取值范围;
的取值范围;(Ⅱ)若集合
 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的角
的角 所对的边份别为
所对的边份别为 ,且
,且
(1)求角
 的大小;
的大小;(2)若
 ,求
,求 的周长
的周长 的取值范围.
的取值范围. -
科目: 来源: 题型:
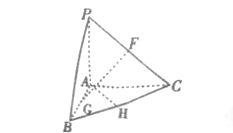
查看答案和解析>>【题目】如图,在三棱锥
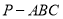 中,
中, 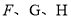 分别是
分别是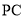 、
、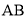 、
、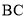 的中点,
的中点, 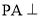 平面
平面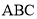 ,
, 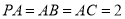 ,二面角
,二面角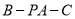 为
为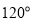 .
.
(1)证明:
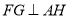 ;
;(2)求二面角
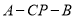 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
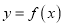 在实数集
在实数集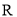 上的图象是连续不断的,且对任意实数
上的图象是连续不断的,且对任意实数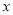 存在常数
存在常数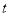 使得
使得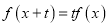 恒成立,则称
恒成立,则称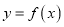 是一个“关于
是一个“关于 函数”.现有下列“关于
函数”.现有下列“关于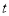 函数”的结论:
函数”的结论:①常数函数是“关于
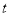 函数”;
函数”;②正比例函数必是一个“关于
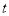 函数”;
函数”;③“关于
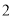 函数”至少有一个零点;
函数”至少有一个零点;④
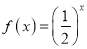 是一个“关于
是一个“关于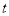 函数”.
函数”.其中正确结论的序号是_______.
相关试题

