Question

【题目】已知椭圆C： 的上下焦点分别为F1 ， F2 ， 离心率为 ，P为C上动点，且满足 |，△QF1F2面积的最大值为4． （Ⅰ）求Q点轨迹E的方程和椭圆C的方程；
（Ⅱ）直线y=kx+m（m＞0）与椭圆C相切且与曲线E交于M，N两点，求 的取值范围．

Answer 1

【答案】解：（Ⅰ）由椭圆定义得：|F2Q|=|F2P|+|PQ|=|F2P|+|PF1|=2a， 所以点Q的轨迹是以F2为圆心，2a为半径的圆．
当QF2⊥F1F2时△QF1F2面积最大，所以 得：ac=2
又 可得a=2，c=1．
所以Q点轨迹E的方程x2+（y+1）2=16，椭圆C的方程
（Ⅱ）由 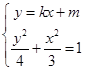得（3k2+4）x2+6kmx+3m2﹣12=0△=36k2m2﹣4（3k2+4）（3m2﹣12）=0
化简得：3k2﹣m2+4=0
所以，
由 及m＞0得，m≥2
设圆心F2（0，﹣1）到直线MN的距离为d，则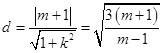
所以，弦长
设点F1（0，1）到直线MN的距离为h，则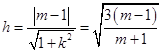
所以，
由m≥2，得：
所以， 的取值范围为 ．
【解析】（Ⅰ）由椭圆定义得：|F2Q|=|F2P|+|PQ|=|F2P|+|PF1|=2a，点Q的轨迹是以F2为圆心，2a为半径的圆，当QF2⊥F1F2时△QF1F2面积最大，推出ac=2，结合离心率，然后求解椭圆方程即可．（Ⅱ）联立 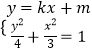通过△=0，推出 求出m≥2，设圆心F2（0，﹣1）到直线MN的距离为d，求出弦长，设点F1（0，1）到直线MN的距离为h，求出三角形的面积的表达式，然后求解范围即可．