【题目】已知函数![]()
![]() 的一段图像如图所示.
的一段图像如图所示.

(1)求此函数的解析式;
(2)求此函数在![]() 上的单调递增区间.
上的单调递增区间.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]() .
.
【解析】
![]() 根据三角函数的图象求出
根据三角函数的图象求出![]() ,
,![]() ,即可确定出函数的解析式
,即可确定出函数的解析式
![]() 根据函数的表达式,即可求出函数的单调递增区间
根据函数的表达式,即可求出函数的单调递增区间
(1)由图可知,其振幅为A=2![]() ,
,
由于![]()
所以周期为T=16,
所以![]()
此时解析式为![]()
因为点(2,-2![]() )在函数
)在函数![]() 的图象上,
的图象上,
所以![]() 所以
所以![]()
又|φ|<π,所以![]()
故所求函数的解析式为![]()
(2)由![]() ,得16k+2≤x≤16k+10(k∈Z),
,得16k+2≤x≤16k+10(k∈Z),
所以函数![]() 的递增区间是[16k+2,16k+10](k∈Z).
的递增区间是[16k+2,16k+10](k∈Z).
当k=-1时,有递增区间[-14,-6],当k=0时,有递增区间[2,10],
与定义区间求交集得此函数在(-2π,2π)上的递增区间为(-2π,-6]和[2,2π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)判断并证明函数
 的奇偶性;
的奇偶性;(2)判断当
 时函数
时函数 的单调性,并用定义证明;
的单调性,并用定义证明;(3)若
 定义域为
定义域为 ,解不等式
,解不等式 .
.【答案】(1)奇函数(2)增函数(3)

【解析】试题分析:(1)判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。(2)利函数单调性定义证明单调性,按假设,作差,化简,判断,下结论五个步骤。(3)由(1)(2)奇函数
 在(-1,1)为单调函数,
在(-1,1)为单调函数,原不等式变形为f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函数的单调性及定义(-1,1)求解得x范围。
试题解析:(1)函数
 为奇函数.证明如下:
为奇函数.证明如下: 定义域为
定义域为
又

 为奇函数
为奇函数 (2)函数
 在(-1,1)为单调函数.证明如下:
在(-1,1)为单调函数.证明如下:任取
 ,则
,则

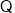
 ,
, 

即

故
 在(-1,1)上为增函数
在(-1,1)上为增函数(3)由(1)、(2)可得
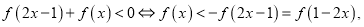 则
则 解得:
解得: 
所以,原不等式的解集为

【点睛】
(1)奇偶性:判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。
(2)单调性:利函数单调性定义证明单调性,按假设,作差,化简,定号,下结论五个步骤。
【题型】解答题
【结束】
22【题目】已知函数
 .
.(1)若
 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数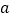 的值;
的值;(2)若
 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,都有
,都有 ,求实数
,求实数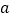 的取值范围;
的取值范围;(3)若
 ,且对任意的
,且对任意的 ,都存在
,都存在 ,使得
,使得 成立,求实数
成立,求实数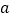 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设实数x,y满足不等式组
 ,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
A.(0,1)
B.(0,1]
C.(﹣∞,﹣2)
D.(﹣∞,﹣2] -
科目: 来源: 题型:
查看答案和解析>>【题目】在图中的算法中,如果输入A=2016,B=98,则输出的结果是 .
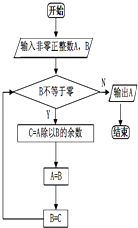
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 上的焦点为
上的焦点为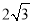 ,离心率为
,离心率为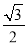 .
.
(1)求椭圆方程;
(2)设过椭圆顶点
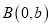 ,斜率为
,斜率为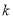 的直线交椭圆于另一点
的直线交椭圆于另一点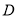 ,交
,交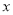 轴于点
轴于点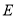 ,且
,且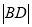 ,
, 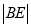 ,
, 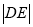 成等比数列,求
成等比数列,求 的值.
的值. -
科目: 来源: 题型:
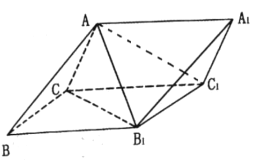
查看答案和解析>>【题目】如图,三棱柱
 中,侧面
中,侧面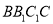 为菱形,
为菱形, 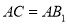 .
.
(1)证明:
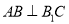 ;
;(2)若
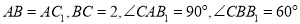 ,求二面角
,求二面角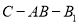 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某运输公司有7辆可载
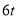 的
的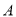 型卡车与4辆可载
型卡车与4辆可载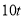 的
的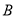 型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运
型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运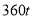 沥青的任务,已知每辆卡车每天往返的次数为
沥青的任务,已知每辆卡车每天往返的次数为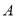 型车8次,
型车8次, 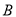 型车6次,每辆卡车每天往返的成本费为
型车6次,每辆卡车每天往返的成本费为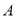 型车160元,
型车160元, 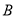 型车252元,每天派出
型车252元,每天派出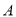 型车和
型车和 型车各多少辆,公司所花的成本费最低?
型车各多少辆,公司所花的成本费最低?
相关试题

