【题目】(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系xOy中,圆C的参数方程![]() 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆C的交点为O、P,与直线
与圆C的交点为O、P,与直线![]() 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
参考答案:
【答案】(1)![]() ;(2)线段
;(2)线段![]() 的长为
的长为![]() .
.
【解析】试题分析:(1)由圆的参数方程消去参数![]() ,得到圆
,得到圆![]() 的普通方程为
的普通方程为![]() ,代入
,代入![]() 得极坐标方程。(2)由
得极坐标方程。(2)由![]() ,而|OP|,|OQ|有极径的几何意义,所以直线
,而|OP|,|OQ|有极径的几何意义,所以直线![]() 的极坐标方程是
的极坐标方程是![]() 中令
中令![]() ,得
,得![]() ,所以
,所以![]() .在
.在![]() 的极坐标方程中令
的极坐标方程中令![]() ,得
,得![]() ,所以
,所以![]() ,
, ![]() .
.
试题解析:(Ⅰ)消去参数![]() ,得到圆
,得到圆![]() 的普通方程为
的普通方程为![]() ,
,
令![]() 代入
代入![]() 的普通方程,
的普通方程,
得![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() .
.
(Ⅱ)在![]() 的极坐标方程中令
的极坐标方程中令![]() ,得
,得![]() ,所以
,所以![]() .
.
在![]() 的极坐标方程中令
的极坐标方程中令![]() ,得
,得![]() ,所以
,所以![]() .
.
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
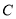 方程为
方程为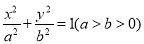 ,双曲线
,双曲线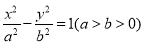 的两条渐近线分别为
的两条渐近线分别为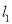 ,
,  ,过椭圆
,过椭圆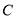 的右焦点作直线
的右焦点作直线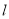 ,使
,使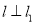 ,又
,又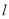 与
与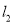 交于点
交于点 ,设直线
,设直线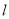 与椭圆
与椭圆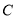 的两个交点由上至下依次为
的两个交点由上至下依次为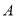 ,
, 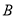 .
. 
(1)若
 与
与 所成的锐角为
所成的锐角为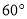 ,且双曲线的焦距为4,求椭圆
,且双曲线的焦距为4,求椭圆 的方程;
的方程;(2)求
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是矩形,平面
是矩形,平面 平面
平面 分别为棱
分别为棱 的中点.求证:
的中点.求证:
(1)
 平面
平面 ;
;(2)
 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,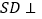 平面
平面 ,四边形
,四边形 是直角梯形,
是直角梯形, .
.
(1)求二面角
 的余弦值;
的余弦值;(2)设
 是棱
是棱 上一点,
上一点, 是
是 的中点,若
的中点,若 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的首项a1=a,其前n项和为Sn , 且满足Sn+Sn﹣1=3n2+2n+4(n≥2),若对任意的n∈N* , an<an+1恒成立,则a的取值范围是( )
A.(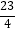 ,
, 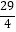 )
)
B.(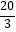 ,
, 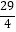 )
)
C.(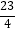 ,
, 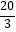 )
)
D.(﹣∞,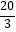 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下说法:①不共面的四点中,任意三点不共线;
②有三个不同公共点的两个平面重合;
③没有公共点的两条直线是异面直线;
④分别和两条异面直线都相交的两条直线异面;
⑤一条直线和两条异面直线都相交,则它们可以确定两个平面.
其中正确结论的序号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,角A,B,C所对边分别为a,b,c,a=2,B=45°,①当b=
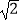 时,三角形有个解;②若三角形有两解,则b的取值范围是 .
时,三角形有个解;②若三角形有两解,则b的取值范围是 .
相关试题

