【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() 分别为棱
分别为棱![]() 的中点.求证:
的中点.求证:

(1)![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
参考答案:
【答案】(1)详见解析; (2)详见解析.
【解析】试题分析:(1)线面平行的证明则只需在面内找一线与之平行即可,因为M,N分别为棱PD,PC的中点,所以MN∥DC, 又因为底面ABCD是矩形,所以AB∥DC,
所以MN∥AB.(2)线面垂直则需要在面内找两根相交线与之垂直,因为AP=AD,M为PD的中点, 所以AM⊥PD.因为平面PAD⊥平面ABCD, 又平面PAD∩平面ABCD= AD,CD⊥AD,![]() 平面ABCD,所以CD⊥平面PAD. 又
平面ABCD,所以CD⊥平面PAD. 又![]() 平面PAD,所以CD⊥AM.
平面PAD,所以CD⊥AM.
试题解析:
(1)因为M,N分别为棱PD,PC的中点,所以MN∥DC, 又因为底面ABCD是矩形,所以AB∥DC,
所以MN∥AB. 又![]() 平面PAB,
平面PAB,![]() 平面PAB,所以MN∥平面PAB.
平面PAB,所以MN∥平面PAB.
(2)因为AP=AD,M为PD的中点, 所以AM⊥PD.因为平面PAD⊥平面ABCD, 又平面PAD∩平面ABCD= AD,CD⊥AD,![]() 平面ABCD,所以CD⊥平面PAD. 又
平面ABCD,所以CD⊥平面PAD. 又![]() 平面PAD,所以CD⊥AM. 因为CD,
平面PAD,所以CD⊥AM. 因为CD,![]() 平面PCD,
平面PCD,![]() ,所以AM⊥平面PCD.
,所以AM⊥平面PCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
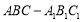 的底面为正三角形,
的底面为正三角形,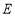 、
、 、
、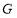 分别是
分别是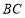 、
、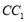 、
、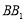 的中点.
的中点.
⑴若
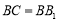 ,求证:
,求证: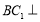 平面
平面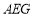 ;
;⑵若
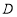 为
为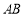 中点,
中点,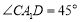 ,四棱锥
,四棱锥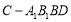 的体积为
的体积为 ,求三棱锥
,求三棱锥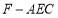 的表面积.
的表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】
已知函数
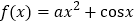 (
(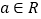 ),记
),记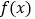 的导函数为
的导函数为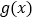 .
.(1)证明:当
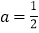 时,
时,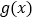 在
在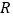 上单调递增;
上单调递增;(2)若
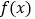 在
在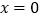 处取得极小值,求
处取得极小值,求 的取值范围;
的取值范围; (3)设函数
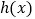 的定义域为
的定义域为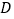 ,区间
,区间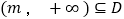 ,若
,若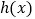 在
在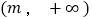 上是单调函数,
上是单调函数,则称
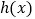 在
在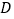 上广义单调.试证明函数
上广义单调.试证明函数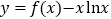 在
在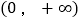 上广义单调.
上广义单调. -
科目: 来源: 题型:
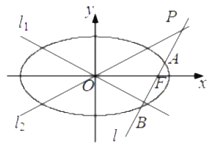
查看答案和解析>>【题目】已知椭圆
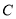 方程为
方程为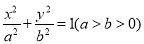 ,双曲线
,双曲线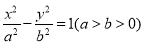 的两条渐近线分别为
的两条渐近线分别为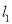 ,
,  ,过椭圆
,过椭圆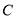 的右焦点作直线
的右焦点作直线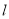 ,使
,使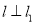 ,又
,又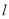 与
与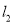 交于点
交于点 ,设直线
,设直线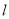 与椭圆
与椭圆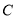 的两个交点由上至下依次为
的两个交点由上至下依次为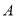 ,
,  .
. 
(1)若
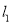 与
与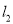 所成的锐角为
所成的锐角为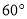 ,且双曲线的焦距为4,求椭圆
,且双曲线的焦距为4,求椭圆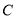 的方程;
的方程;(2)求
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,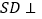 平面
平面 ,四边形
,四边形 是直角梯形,
是直角梯形, .
.
(1)求二面角
 的余弦值;
的余弦值;(2)设
 是棱
是棱 上一点,
上一点, 是
是 的中点,若
的中点,若 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系xOy中,圆C的参数方程
 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.(1)求圆C的极坐标方程;
(2)直线
 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆C的交点为O、P,与直线
与圆C的交点为O、P,与直线 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的首项a1=a,其前n项和为Sn , 且满足Sn+Sn﹣1=3n2+2n+4(n≥2),若对任意的n∈N* , an<an+1恒成立,则a的取值范围是( )
A.(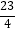 ,
, 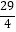 )
)
B.(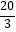 ,
, 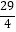 )
)
C.(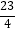 ,
, 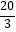 )
)
D.(﹣∞,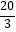 )
)
相关试题

