搜索
【题目】在锐角△ABC的内角A，B，C的对边分别为a，b，c，且 
a=2csinA．
（1）确定角C的大小；
（2）若c= 
，且ab=6，求边a，b．
参考答案：
【答案】
（1）解：由 
a=2csinA及正弦定理得 
= 
= 
，
因为sinA＞0，故sinC= 
，
又锐角△ABC，所以C= 
．
（2）解：由余弦定理a2+b2﹣2abcos =7， ab=6，得a2+b2=1，
解得： 
或 
．
【解析】（1）由已知及正弦定理得 = = ，结合sinA＞0，可求sinC= ，根据已知可求C= ．（2）由余弦定理，ab=6，可求a2+b2=1，联立即可解得a，b的值．
【考点精析】利用正弦定理的定义和余弦定理的定义对题目进行判断即可得到答案，需要熟知正弦定理:
；余弦定理:
;
;
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC的内角A，B，C的对边分别为a，b，c，若cosA=
，c=3b，且△ABC面积S△ABC= 
．
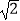（1）求边b．c；
（2）求边a并判断△ABC的形状． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，矩形ABCD的一边AB在x轴上，另一边CD在x轴上方，且AB=8，BC=6，其中A（﹣4，0）、B（4，0）．
（1）若A、B为椭圆的焦点，且椭圆经过C、D两点，求该椭圆的方程；
（2）若A、B为双曲线的焦点，且双曲线经过C、D两点，求双曲线的方程． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，设命题p：椭圆C：
+ 
=1的焦点在x轴上；命题q：直线l：x﹣y+m=0与圆O：x2+y2=9有公共点． 若命题p、命题q中有且只有一个为真命题，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】某学校实行自主招生，参加自主招生的学生从8个试题中随机挑选出4个进行作答，至少答对3个才能通过初试．已知甲、乙两人参加初试，在这8个试题中甲能答对6个，乙能答对每个试题的概率为
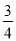，且甲、乙两人是否答对每个试题互不影响．（Ⅰ）求甲通过自主招生初试的概率；
（Ⅱ）试通过概率计算，分析甲、乙两人谁通过自主招生初试的可能性更大；
（Ⅲ）记甲答对试题的个数为
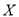，求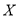
的分布列及数学期望． -
科目： 来源： 题型：
查看答案和解析>>【题目】设等比数列{an}的各项均为正数，其前n项和为Sn ， 若a1=1，a3=4．
（1）若Sk=63，求k的值；
（2）设bn=log2an ， 证明数列{bn}是等差数列；
（3）设cn=（﹣1）nbn ， 求T=|c1|+|c2|+|c3|+…+|cn|． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
（
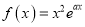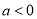）.（1）若
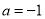，求曲线
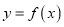在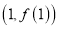
处的切线方程；（2）若对任意
， 
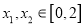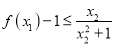恒成立，求实数
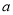的取值范围.
相关试题
