【题目】已知函数![]() (
(![]() ).
).
(1)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若对任意![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析: ![]() 由导函数研究切线的斜率可得切线方程为
由导函数研究切线的斜率可得切线方程为![]()
![]() 令
令![]() ,结合函数的性质分类讨论
,结合函数的性质分类讨论![]() 和
和![]() 两种情况可得实数
两种情况可得实数![]() 的取值范围。
的取值范围。
解析:(1)依题意, ![]() ,
, ![]() ,故
,故![]() ,
,
又![]() ,故所求切线方程为
,故所求切线方程为![]() ,即
,即![]() ;
;
(2)令![]() ,故函数
,故函数![]() 的定义域为
的定义域为![]() ,
, 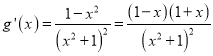 .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| 单调减 | 单调增 | 单调减 |
因为![]() ,
, ![]() ,所以
,所以![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
因为![]() . 因为
. 因为![]() ,令
,令![]() 得,
得, ![]() ,
, ![]() .
.
(ⅰ)当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,所以函数
上单调递增,所以函数![]() .由
.由![]() 得,
得, ![]() ,所以
,所以![]() .
.
(ⅱ)当![]() ,即
,即![]() 时, 在
时, 在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]() ,由
,由![]() 得,
得, ![]() ,所以
,所以![]() .
.
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角△ABC的内角A,B,C的对边分别为a,b,c,且
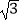 a=2csinA.
a=2csinA.
(1)确定角C的大小;
(2)若c=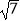 ,且ab=6,求边a,b.
,且ab=6,求边a,b. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校实行自主招生,参加自主招生的学生从8个试题中随机挑选出4个进行作答,至少答对3个才能通过初试.已知甲、乙两人参加初试,在这8个试题中甲能答对6个,乙能答对每个试题的概率为
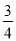 ,且甲、乙两人是否答对每个试题互不影响.
,且甲、乙两人是否答对每个试题互不影响.(Ⅰ)求甲通过自主招生初试的概率;
(Ⅱ)试通过概率计算,分析甲、乙两人谁通过自主招生初试的可能性更大;
(Ⅲ)记甲答对试题的个数为
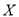 ,求
,求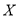 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设等比数列{an}的各项均为正数,其前n项和为Sn , 若a1=1,a3=4.
(1)若Sk=63,求k的值;
(2)设bn=log2an , 证明数列{bn}是等差数列;
(3)设cn=(﹣1)nbn , 求T=|c1|+|c2|+|c3|+…+|cn|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多面体
 如图所示,底面
如图所示,底面 为矩形,其中
为矩形,其中 平面
平面 ,
, 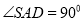 ,若
,若 分别是
分别是 的中心,其中
的中心,其中 .
.
(1)证明:
 ;
;(2)若二面角
 的余弦值为
的余弦值为 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正三棱柱
 中,
中,  ,
, 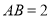 ,
,  为棱
为棱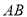 的中点.
的中点.
(
 )求证:
)求证:  平面
平面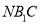 .
.(
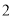 )求证:平面
)求证:平面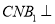 平面
平面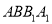 .
.(
 )求四棱锥
)求四棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点
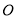 为极点,
为极点, 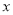 轴的正半轴为极轴建立坐标系,已知点
轴的正半轴为极轴建立坐标系,已知点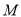 的直角坐标为
的直角坐标为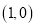 ,若直线
,若直线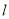 的极坐标方程为
的极坐标方程为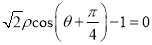 .曲线
.曲线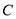 的参数方程是
的参数方程是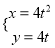 (
(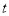 为参数).
为参数).(1)求直线
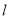 和曲线
和曲线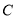 的普通方程;
的普通方程;(2)设直线
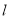 和曲线
和曲线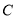 交于
交于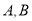 两点,求
两点,求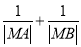 .
.
相关试题

