【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,若cosA= ![]() ,c=3b,且△ABC面积S△ABC=
,c=3b,且△ABC面积S△ABC= ![]() .
.
(1)求边b.c;
(2)求边a并判断△ABC的形状.
参考答案:
【答案】
(1)解:∵cos A= ![]() ,
,
∴sin A= ![]() .又S△ABC=
.又S△ABC= ![]() bcsin A=
bcsin A= ![]() ,
,
∴bc=3.又c=3b,
∴b=1,c=3.
(2)解:由余弦定理a2=b2+c2﹣2bccosA,得:a2=1+9﹣2× ![]() =8,
=8,
故a=2 ![]() .
.
由c2=a2+b2知△ABC为直角三角形.
【解析】(1)由已知利用同角三角函数基本关系式可求sinA,利用三角形面积公式可求bc的值,又c=3b,即可解得b,c的值.(2)由余弦定理可求a的值,由勾股定理即可得解△ABC为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“糖尿病”已经成为日渐多发的一种疾病,其具有危害性大且难以完全治愈的特征.为了更好的抑制“糖尿病”多发的势头,某社区卫生医疗机构针对所服务居民开展了免费测血糖活动,将随机抽取的10名居民均分为
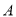 ,
, 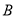 两组(
两组(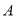 组:4.3,5.1,4.6,4.1,4.9;
组:4.3,5.1,4.6,4.1,4.9; 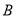 组:5.1,4.9,4.0,4.0,4.5).
组:5.1,4.9,4.0,4.0,4.5).(1)通过提供的数据请判断哪一组居民的血糖值更低;
(2)现从
 组的5名居民中随机选取2名,求这2名中至少有1名的血糖值低于4.5的概率.
组的5名居民中随机选取2名,求这2名中至少有1名的血糖值低于4.5的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点
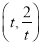 (
( ,且
,且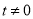 )为圆心的圆与
)为圆心的圆与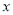 轴交于点
轴交于点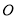 ,
, 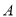 ,与
,与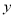 轴交于点
轴交于点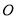 ,
, 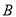 ,其中
,其中 为坐标原点.
为坐标原点.(1)求证:
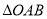 的面积为定值;
的面积为定值;(2)设直线
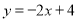 与圆
与圆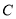 交于点
交于点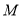 ,
, 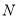 ,若
,若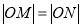 ,求圆
,求圆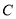 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】若点(x,y)在双曲线
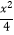 ﹣y2=1上,则3x2﹣2xy的最小值是 .
﹣y2=1上,则3x2﹣2xy的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,矩形ABCD的一边AB在x轴上,另一边CD在x轴上方,且AB=8,BC=6,其中A(﹣4,0)、B(4,0).

(1)若A、B为椭圆的焦点,且椭圆经过C、D两点,求该椭圆的方程;
(2)若A、B为双曲线的焦点,且双曲线经过C、D两点,求双曲线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,设命题p:椭圆C:
 +
+  =1的焦点在x轴上;命题q:直线l:x﹣y+m=0与圆O:x2+y2=9有公共点. 若命题p、命题q中有且只有一个为真命题,求实数m的取值范围.
=1的焦点在x轴上;命题q:直线l:x﹣y+m=0与圆O:x2+y2=9有公共点. 若命题p、命题q中有且只有一个为真命题,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角△ABC的内角A,B,C的对边分别为a,b,c,且
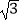 a=2csinA.
a=2csinA.
(1)确定角C的大小;
(2)若c=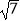 ,且ab=6,求边a,b.
,且ab=6,求边a,b.
相关试题

