【题目】在平面直角坐标系xOy中,设命题p:椭圆C: ![]() +
+ ![]() =1的焦点在x轴上;命题q:直线l:x﹣y+m=0与圆O:x2+y2=9有公共点. 若命题p、命题q中有且只有一个为真命题,求实数m的取值范围.
=1的焦点在x轴上;命题q:直线l:x﹣y+m=0与圆O:x2+y2=9有公共点. 若命题p、命题q中有且只有一个为真命题,求实数m的取值范围.
参考答案:
【答案】解:命题p为真:由题意得,m>8﹣m>0,解得4<m<8.
命题q为真:x﹣y+m=0与圆O:x2+y2=9有公共点
则圆心O到直线l的距离:d= ![]() ≤3,
≤3,
解得:﹣3 ![]() ≤m≤3
≤m≤3 ![]() .
.
因为命题p、命题q中有且只有一个为真命题
若p真q假,则: 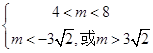 解得:3
解得:3 ![]() <m<8.
<m<8.
若p假q真,则: 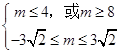 解得:﹣3
解得:﹣3 ![]() ≤m≤4
≤m≤4
综上:实数m的取值范围是3 ![]() <m<8或﹣3
<m<8或﹣3 ![]() ≤m≤4.
≤m≤4.
【解析】求出命题p,q为真时,m的范围,结合命题p、命题q中有且只有一个为真命题,分类讨论,综合后可得实数m的取值范围.
【考点精析】认真审题,首先需要了解命题的真假判断与应用(两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(x,y)在双曲线
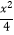 ﹣y2=1上,则3x2﹣2xy的最小值是 .
﹣y2=1上,则3x2﹣2xy的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,若cosA=
 ,c=3b,且△ABC面积S△ABC=
,c=3b,且△ABC面积S△ABC= 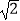 .
.
(1)求边b.c;
(2)求边a并判断△ABC的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,矩形ABCD的一边AB在x轴上,另一边CD在x轴上方,且AB=8,BC=6,其中A(﹣4,0)、B(4,0).

(1)若A、B为椭圆的焦点,且椭圆经过C、D两点,求该椭圆的方程;
(2)若A、B为双曲线的焦点,且双曲线经过C、D两点,求双曲线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角△ABC的内角A,B,C的对边分别为a,b,c,且
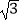 a=2csinA.
a=2csinA.
(1)确定角C的大小;
(2)若c=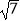 ,且ab=6,求边a,b.
,且ab=6,求边a,b. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校实行自主招生,参加自主招生的学生从8个试题中随机挑选出4个进行作答,至少答对3个才能通过初试.已知甲、乙两人参加初试,在这8个试题中甲能答对6个,乙能答对每个试题的概率为
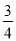 ,且甲、乙两人是否答对每个试题互不影响.
,且甲、乙两人是否答对每个试题互不影响.(Ⅰ)求甲通过自主招生初试的概率;
(Ⅱ)试通过概率计算,分析甲、乙两人谁通过自主招生初试的可能性更大;
(Ⅲ)记甲答对试题的个数为
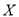 ,求
,求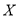 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设等比数列{an}的各项均为正数,其前n项和为Sn , 若a1=1,a3=4.
(1)若Sk=63,求k的值;
(2)设bn=log2an , 证明数列{bn}是等差数列;
(3)设cn=(﹣1)nbn , 求T=|c1|+|c2|+|c3|+…+|cn|.
相关试题

