【题目】某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线![]() .根据图中数据,下列对该样本描述错误的是( )
.根据图中数据,下列对该样本描述错误的是( )
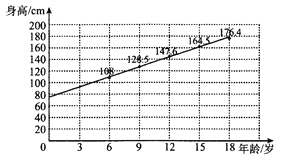
A. 据样本数据估计,该地区青少年身高与年龄成正相关
B. 所抽取数据中,5000名青少年平均身高约为![]()
C. 直线![]() 的斜率的值近似等于样本中青少年平均身高每年的增量
的斜率的值近似等于样本中青少年平均身高每年的增量
D. 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线![]() 上
上
参考答案:
【答案】D
【解析】在给定范围内,随着年龄增加,年龄越大身高越高,故该地区青少年身高与年龄成正相关,故A正确;用样本数据估计总体可得平均数大约是![]() ,故B正确;根据直线斜率的意义可知斜率的值近似等于样本中青少年平均身高每年的增量,故C正确;各取一人具有随机性,根据数据做出的点只能在直线附近,不一定在直线上,故D错误,故选D.
,故B正确;根据直线斜率的意义可知斜率的值近似等于样本中青少年平均身高每年的增量,故C正确;各取一人具有随机性,根据数据做出的点只能在直线附近,不一定在直线上,故D错误,故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区提倡低碳生活,环保出行,在小区提供自行车出租.该小区有40辆自行车供小区住户租赁使用,管理这些自行车的费用是每日92元,根据经验,若每辆自行车的日租金不超过5元,则自行车可以全部出租,若超过5元,则每超过1元,租不出的自行车就增加2辆,为了便于结算,每辆自行车的日租金x元只取整数,用f(x)元表示出租自行车的日纯收入(日纯收入=一日出租自行车的总收入﹣管理费用)
(1)求函数f(x)的解析式及其定义域;
(2)当租金定为多少时,才能使一天的纯收入最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
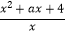 (a>0).
(a>0).
(1)证明函数f(x)在(0,2]上是减函数,(2,+∞)上是增函数;
(2)若方程f(x)=0有且只有一个实数根,判断函数g(x)=f(x)﹣4的奇偶性;
(3)在(2)的条件下探求方程f(x)=m(m≥8)的根的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】设m,n是两条不同的直线,α,β是两个不重合的平面,给定下列四个命题,其中为真命题的是( ) ①
 ;②
;②  ;
;
③ ;④
;④  .
.
A.①和②
B.②和③
C.③和④
D.①和④ -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知
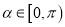 ,在直角坐标系
,在直角坐标系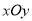 中,直线
中,直线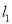 的参数方程为
的参数方程为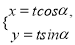 (
(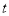 为参数);在以坐标原点
为参数);在以坐标原点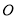 为极点,
为极点, 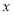 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线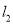 的极坐标方程是
的极坐标方程是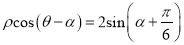 .
.(Ⅰ)求证:
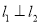 ;
;(Ⅱ)设点
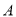 的极坐标为
的极坐标为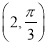 ,
,  为直线
为直线 ,
, 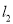 的交点,求
的交点,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
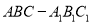 中,侧棱
中,侧棱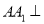 底面
底面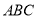 ,
, 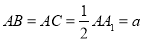 ,
, 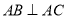 ,
, 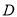 是棱
是棱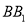 的中点.
的中点.(Ⅰ)证明:平面
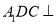 平面
平面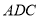 ;
;(Ⅱ)求平面
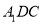 将此三棱柱分成的两部分的体积之比.
将此三棱柱分成的两部分的体积之比.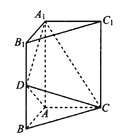
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
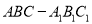 中,侧面
中,侧面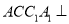 底面
底面 ,
, 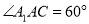 ,
, 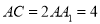 ,点
,点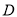 ,
, 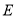 分别是
分别是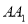 ,
, 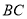 的中点.
的中点.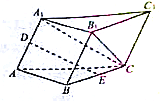
(1)证明:
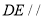 平面
平面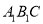 ;
;(2)若
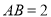 ,
, 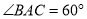 ,求直线
,求直线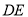 与平面
与平面 所成角的正弦值.
所成角的正弦值.
相关试题

