【题目】某小区提倡低碳生活,环保出行,在小区提供自行车出租.该小区有40辆自行车供小区住户租赁使用,管理这些自行车的费用是每日92元,根据经验,若每辆自行车的日租金不超过5元,则自行车可以全部出租,若超过5元,则每超过1元,租不出的自行车就增加2辆,为了便于结算,每辆自行车的日租金x元只取整数,用f(x)元表示出租自行车的日纯收入(日纯收入=一日出租自行车的总收入﹣管理费用)
(1)求函数f(x)的解析式及其定义域;
(2)当租金定为多少时,才能使一天的纯收入最大?
参考答案:
【答案】
(1)解:由题意:当0<x≤5且x∈N*时,f(x)=40x﹣92
当x>5且x∈N*时,f(x)=[40﹣2(x﹣5)]x﹣92=﹣2x2+50x﹣92
∴ ![]()
其定义域为{x|x∈N*且x≤40}
(2)解:当0<x≤5且x∈N*时,f(x)=40x﹣92,
∴当x=5时,f(x)max=108(元)
当x>5且x∈N*时,f(x)=﹣2x2+50x﹣92=﹣2(x﹣ ![]() )2+
)2+ ![]()
∵开口向下,对称轴为x= ![]() ,
,
又∵x∈N*,∴当x=12或13时f(x)max=220(元)
∵220>108,∴当租金定为12元或13元时,一天的纯收入最大为220元
【解析】(1)利用函数关系建立各个取值范围内的净收入与日租金的关系式,写出该分段函数,是解决该题的关键,注意实际问题中的自变量取值范围;(2)利用一次函数,二次函数的单调性解决该最值问题是解决本题的关键.注意自变量取值区间上的函数类型.应取每段上最大值的较大的即为该函数的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过点
 作一直线与抛物线
作一直线与抛物线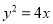 交于
交于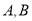 两点,点
两点,点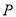 是抛物线
是抛物线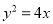 上到直线
上到直线 :
: 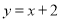 的距离最小的点,直线
的距离最小的点,直线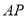 与直线
与直线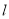 交于点
交于点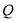 .
.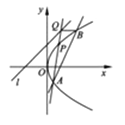
(Ⅰ)求点
 的坐标;
的坐标;(Ⅱ)求证:直线
 平行于抛物线的对称轴.
平行于抛物线的对称轴. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆G:x2﹣x+y2=0,经过抛物线y2=2px的焦点,过点(m,0)(m<0)倾斜角为
 的直线l交抛物线于C,D两点. (Ⅰ)求抛物线的方程;
的直线l交抛物线于C,D两点. (Ⅰ)求抛物线的方程;
(Ⅱ)若焦点F在以线段CD为直径的圆E的外部,求m的取值范围.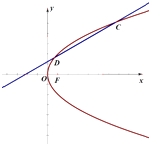
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
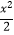 +y2=1的左右焦点分别为F1 , F2 , 直线l过椭圆的右焦点F2与椭圆交于A,B 两点, (Ⅰ)当直线l的斜率为1,点P为椭圆上的动点,满足使得△ABP的面积为
+y2=1的左右焦点分别为F1 , F2 , 直线l过椭圆的右焦点F2与椭圆交于A,B 两点, (Ⅰ)当直线l的斜率为1,点P为椭圆上的动点,满足使得△ABP的面积为 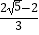 的点P有几个?并说明理由.
的点P有几个?并说明理由.
(Ⅱ)△ABF1的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时直线l的方程,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
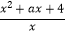 (a>0).
(a>0).
(1)证明函数f(x)在(0,2]上是减函数,(2,+∞)上是增函数;
(2)若方程f(x)=0有且只有一个实数根,判断函数g(x)=f(x)﹣4的奇偶性;
(3)在(2)的条件下探求方程f(x)=m(m≥8)的根的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】设m,n是两条不同的直线,α,β是两个不重合的平面,给定下列四个命题,其中为真命题的是( ) ①
 ;②
;②  ;
;
③ ;④
;④  .
.
A.①和②
B.②和③
C.③和④
D.①和④ -
科目: 来源: 题型:
查看答案和解析>>【题目】某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线
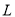 .根据图中数据,下列对该样本描述错误的是( )
.根据图中数据,下列对该样本描述错误的是( )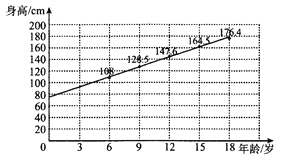
A. 据样本数据估计,该地区青少年身高与年龄成正相关
B. 所抽取数据中,5000名青少年平均身高约为
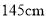
C. 直线
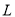 的斜率的值近似等于样本中青少年平均身高每年的增量
的斜率的值近似等于样本中青少年平均身高每年的增量D. 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线
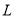 上
上
相关试题

