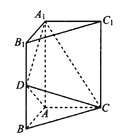
【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 的中点.
的中点.
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 将此三棱柱分成的两部分的体积之比.
将此三棱柱分成的两部分的体积之比.
参考答案:
【答案】(1)平面![]() 平面
平面![]() ;(2)
;(2)![]()
【解析】试题分析:(Ⅰ)通过线面垂直可得![]() ,运用勾股定理可得
,运用勾股定理可得![]() ,由线面垂直判定定理可得
,由线面垂直判定定理可得![]() 平面
平面![]() ,由面面垂直判定定理得结论;(Ⅱ)平面
,由面面垂直判定定理得结论;(Ⅱ)平面![]() 将三棱柱分成上、下两部分,其上面部分几何体为四棱锥
将三棱柱分成上、下两部分,其上面部分几何体为四棱锥![]() ,下面部分几何体为四棱锥
,下面部分几何体为四棱锥![]() ,分别计算出其体积即可.
,分别计算出其体积即可.
试题解析:(Ⅰ)在三棱柱中,有![]() ,
,
又因为![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
,
由![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 的中点.
的中点.
所以![]() ,
, ![]() ,
,
则![]()
![]() ,
,
所以![]() ,
,
因![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
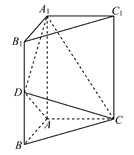
(Ⅱ)平面![]() 将三棱柱分成上、下两部分,其上面部分几何体为四棱锥
将三棱柱分成上、下两部分,其上面部分几何体为四棱锥![]() ,下面部分几何体为四棱锥
,下面部分几何体为四棱锥![]() .
.
在平面![]() 中,过点
中,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 平面
平面![]() ,
,
所以![]() 是四棱锥
是四棱锥![]() 的高,
的高,
在![]() 中,因为
中,因为![]() ,所以
,所以![]() .
.
![]() 为直角梯形,其面积
为直角梯形,其面积![]()
![]() ,
,
所以四棱锥![]() 的体积
的体积![]()
![]() .
.
因三棱柱![]() 的体积
的体积![]()
![]() ,
,
所以下部分几何体![]() 的体积
的体积![]()
![]() ,
,
所以两部分几何体的体积之比为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设m,n是两条不同的直线,α,β是两个不重合的平面,给定下列四个命题,其中为真命题的是( ) ①
 ;②
;②  ;
;
③ ;④
;④  .
.
A.①和②
B.②和③
C.③和④
D.①和④ -
科目: 来源: 题型:
查看答案和解析>>【题目】某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线
 .根据图中数据,下列对该样本描述错误的是( )
.根据图中数据,下列对该样本描述错误的是( )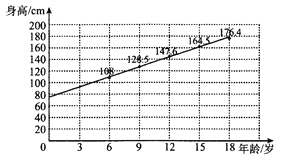
A. 据样本数据估计,该地区青少年身高与年龄成正相关
B. 所抽取数据中,5000名青少年平均身高约为
C. 直线
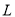 的斜率的值近似等于样本中青少年平均身高每年的增量
的斜率的值近似等于样本中青少年平均身高每年的增量D. 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线
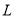 上
上 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知
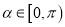 ,在直角坐标系
,在直角坐标系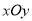 中,直线
中,直线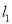 的参数方程为
的参数方程为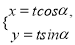 (
(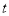 为参数);在以坐标原点
为参数);在以坐标原点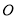 为极点,
为极点, 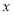 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线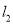 的极坐标方程是
的极坐标方程是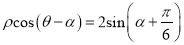 .
.(Ⅰ)求证:
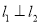 ;
;(Ⅱ)设点
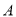 的极坐标为
的极坐标为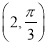 ,
,  为直线
为直线 ,
, 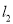 的交点,求
的交点,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
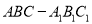 中,侧面
中,侧面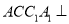 底面
底面 ,
, 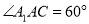 ,
, 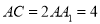 ,点
,点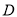 ,
, 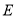 分别是
分别是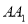 ,
, 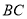 的中点.
的中点.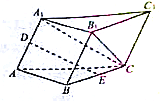
(1)证明:
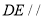 平面
平面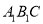 ;
;(2)若
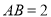 ,
, 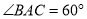 ,求直线
,求直线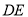 与平面
与平面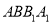 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①BC⊥PC;②OM∥平面APC;③点B到平面PAC的距离等于线段BC的长.其中真命题的个数为( )

A.3
B.2
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
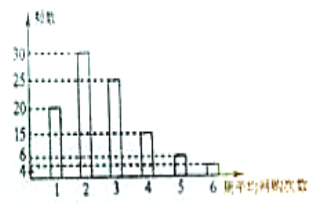
(1)根据已知条件完成下面的
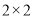 列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?网购迷
非网购迷
合计
年龄不超过40岁
年龄超过40岁
合计
(2)若从网购迷中任意选取2名,求其中年龄超过40岁的市民人数
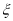 的分布列与期望.
的分布列与期望.附:
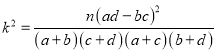 ;
;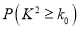
0.15
0.10
0.05
0.01
2.072
2.706
3.841
6.635
相关试题

