【题目】某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2 . (不计木料的粗细与接头处损耗) 
(1)如何设计外框的长与宽,才能使外框矩形面积最小?
(2)如何设计外框的长与宽,才能使制作整个展示框所用木条最少?
参考答案:
【答案】
(1)解:设展示框外框的长为xcm,宽为ycm,则内框长为(x﹣16)cm,宽为(y﹣8)cm,由题意x>16,y>8,因为内框的面积为3200cm2,所以(x﹣16)(y﹣8)=3200,所以 ![]() ,外框面积为S=xy=8x+
,外框面积为S=xy=8x+ ![]() =3328+8(x﹣16)+
=3328+8(x﹣16)+ ![]() ,因为x>16,所以x﹣16>0,所以S≥3328+2
,因为x>16,所以x﹣16>0,所以S≥3328+2 ![]() =3328+1280=4608,当且仅当8(x﹣16)=
=3328+1280=4608,当且仅当8(x﹣16)= ![]() 即x=96时等号成立,
即x=96时等号成立,
所以外框的长与宽分别是96cm,48cm时,才能使外框矩形面积最小
(2)解:由(1)可知,所用木条的总长度为4(x+y)=4(x+8+ ![]() )=4(x﹣16+
)=4(x﹣16+ ![]() +24)≥4(2
+24)≥4(2 ![]() +24)=96+320
+24)=96+320 ![]() ,当且仅当x﹣16=
,当且仅当x﹣16= ![]() 即x=16+40
即x=16+40 ![]() ,y=8+40
,y=8+40 ![]() 时等号成立;
时等号成立;
所以外框的长与宽分别是(16+40 ![]() )cm,(8+40
)cm,(8+40 ![]() )cm时,才能使制作整个展示框所用木条最少
)cm时,才能使制作整个展示框所用木条最少
【解析】(1)设展示框外框的长为xcm,宽为ycm,则内框长为(x﹣16)cm,宽为(y﹣8)cm,利用x,y表示面积,列出面积表达式,变形,利用基本不等式求其最小值;(2)利用(1)得到木条的长度表达式,变形,结合基本不等式求最小值.
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识,掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算求值.
(1)已知cosα=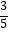 ,α为锐角,求tan2α的值;
,α为锐角,求tan2α的值;
(2)已知sin(θ+ )=
)= 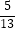 ,θ为钝角,求cosθ的值.
,θ为钝角,求cosθ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直四棱柱ABCD﹣A1B1C1D1的底面ABCD为菱形,且∠BCD=60°,P为AD1的中点,Q为BC的中点

(1)求证:PQ∥平面D1DCC1;
(2)求证:DQ⊥平面B1BCC1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
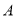 为椭圆
为椭圆 上的一个动点,弦
上的一个动点,弦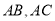 分别过左右焦点
分别过左右焦点 ,且当线段
,且当线段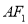 的中点在
的中点在 轴上时,
轴上时, 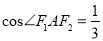 .
.(1)求该椭圆的离心率;(2)设
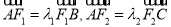 ,试判断
,试判断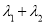 是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①已知集合A={1,a},B={1,2,3},则“a=3”是“AB”的充分不必要条件;
②“x<0”是“ln(x+1)<0”的必要不充分条件;
③“函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的充要条件;
④“平面向量 与
与 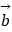 的夹角是钝角”的充要条件的“
的夹角是钝角”的充要条件的“ 
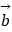 <0”.
<0”.
其中正确命题的序号是(把所有正确命题的序号都写上) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于
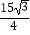 ,D为边长BC上一点.
,D为边长BC上一点. 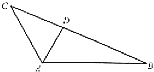
(1)求BC的长;
(2)当AD=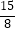 时,求cos∠CAD的值.
时,求cos∠CAD的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两艘轮船都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随机到达,则这两艘船中至少有一艘在停靠泊位时必须等待的概率是 .
相关试题

