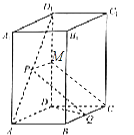
【题目】如图,已知直四棱柱ABCD﹣A1B1C1D1的底面ABCD为菱形,且∠BCD=60°,P为AD1的中点,Q为BC的中点 
(1)求证:PQ∥平面D1DCC1;
(2)求证:DQ⊥平面B1BCC1 .
参考答案:
【答案】
(1)证明:过P作PM∥AD交D1D于M,连接MC,则M为D1D的中点,
∴PM∥AD,PM= ![]() AD,
AD,
∵AD∥BC,Q为BC的中点,
∴PM∥QC,PM=QC,
∴四边形PMCQ是平行四边形,
∴PQ∥MC,
∵PQ平面DCC1D1,MC平面DCC1D1,
∴PQ∥平面DCC1D1
(2)解:在直四棱柱ABCD﹣A1B1C1D1中,B1B⊥平面ABCD,DQ平面ABCD,
∴B1B⊥DQ,
在菱形ABCD中,DC=BC,∠BCD=60°,∴△BCD为正三角形,故DB=DC,
∵Q为BC的中点,
∴DQ⊥BC,
∵B1B∩BC=B,
∴DQ⊥平面B1BCC1.
【解析】(1)过P作PM∥AD交D1D于M,连接MC,则M为D1D的中点,证明四边形PMCQ是平行四边形,可得PQ∥MC,即可证明PQ∥平面D1DCC1;(2)证明B1B⊥DQ,DQ⊥BC,利用线面垂直的判定定理证明:DQ⊥平面B1BCC1 .
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
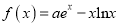 ,其中
,其中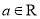 ,
, 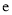 是自然对数的底数.
是自然对数的底数.(Ⅰ)若
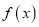 是
是 上的增函数,求
上的增函数,求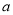 的取值范围;
的取值范围;(Ⅱ)若
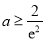 ,证明:
,证明: 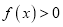 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知点A(2,4),直线l:x﹣2y+1=0.
(1)求过点A且平行于l的直线的方程;
(2)若点M在直线l上,且AM⊥l,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算求值.
(1)已知cosα=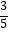 ,α为锐角,求tan2α的值;
,α为锐角,求tan2α的值;
(2)已知sin(θ+ )=
)= 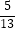 ,θ为钝角,求cosθ的值.
,θ为钝角,求cosθ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
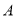 为椭圆
为椭圆 上的一个动点,弦
上的一个动点,弦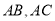 分别过左右焦点
分别过左右焦点 ,且当线段
,且当线段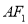 的中点在
的中点在 轴上时,
轴上时, 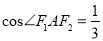 .
.(1)求该椭圆的离心率;(2)设
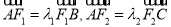 ,试判断
,试判断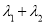 是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2 . (不计木料的粗细与接头处损耗)

(1)如何设计外框的长与宽,才能使外框矩形面积最小?
(2)如何设计外框的长与宽,才能使制作整个展示框所用木条最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①已知集合A={1,a},B={1,2,3},则“a=3”是“AB”的充分不必要条件;
②“x<0”是“ln(x+1)<0”的必要不充分条件;
③“函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的充要条件;
④“平面向量 与
与 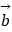 的夹角是钝角”的充要条件的“
的夹角是钝角”的充要条件的“ 
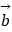 <0”.
<0”.
其中正确命题的序号是(把所有正确命题的序号都写上)
相关试题

