【题目】已知![]() 为椭圆
为椭圆![]() 上的一个动点,弦
上的一个动点,弦![]() 分别过左右焦点
分别过左右焦点![]() ,且当线段
,且当线段![]() 的中点在
的中点在![]() 轴上时,
轴上时, ![]() .
.
(1)求该椭圆的离心率;(2)设![]() ,试判断
,试判断![]() 是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
参考答案:
【答案】(1)![]() (2)
(2)![]() 是定值6.
是定值6.
【解析】试题分析:(1)当线段![]() 的中点在y轴上时,AC垂直于x轴,
的中点在y轴上时,AC垂直于x轴, ![]() 为直角三角形.运用余弦函数的定义可得
为直角三角形.运用余弦函数的定义可得![]() ,易知
,易知![]() ,再由椭圆的定义,结合离心率公式即可得到所求值;
,再由椭圆的定义,结合离心率公式即可得到所求值;
(2)由(1)得椭圆方程为![]() ,焦点坐标为
,焦点坐标为![]() ,当AB,AC的斜率都存在时,设
,当AB,AC的斜率都存在时,设![]() ,求得直线AC的方程,代入椭圆方程,运用韦达定理,再由向量共线定理,可得
,求得直线AC的方程,代入椭圆方程,运用韦达定理,再由向量共线定理,可得![]() 为定值6;若
为定值6;若![]() 轴,若
轴,若![]() 轴,计算即可得到所求定值.
轴,计算即可得到所求定值.
试题解析:
解:(1)当线段![]() 的中点在
的中点在![]() 轴上时,
轴上时, ![]() 垂直于
垂直于![]() 轴,
轴, ![]() 为直角三角形,
为直角三角形,
因为![]() ,所以
,所以![]() ,
,
易知![]() ,
,
由椭圆的定义可得![]() ,
,
则![]() ,即
,即![]() ;即
;即![]() ,即有
,即有![]() ;
;
(2)由(1)得椭圆方程为![]() ,焦点坐标为
,焦点坐标为![]() ,
,
①当![]() 的斜率都存在时,设
的斜率都存在时,设![]() ,
,
则直线![]() 的方程为
的方程为![]() ,代入椭圆方程得:
,代入椭圆方程得:
![]() ,
,
可得![]() ,又
,又 ,
,
同理![]() ,可得
,可得![]() ;
;
(2)若![]() 轴,则
轴,则![]() ,
, ![]() ,这时
,这时![]() ;
;
若![]() 轴,则
轴,则![]() ,这时也有
,这时也有![]() ;
;
综上所述, ![]() 是定值6.
是定值6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知点A(2,4),直线l:x﹣2y+1=0.
(1)求过点A且平行于l的直线的方程;
(2)若点M在直线l上,且AM⊥l,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算求值.
(1)已知cosα=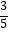 ,α为锐角,求tan2α的值;
,α为锐角,求tan2α的值;
(2)已知sin(θ+ )=
)= 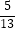 ,θ为钝角,求cosθ的值.
,θ为钝角,求cosθ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直四棱柱ABCD﹣A1B1C1D1的底面ABCD为菱形,且∠BCD=60°,P为AD1的中点,Q为BC的中点

(1)求证:PQ∥平面D1DCC1;
(2)求证:DQ⊥平面B1BCC1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2 . (不计木料的粗细与接头处损耗)

(1)如何设计外框的长与宽,才能使外框矩形面积最小?
(2)如何设计外框的长与宽,才能使制作整个展示框所用木条最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①已知集合A={1,a},B={1,2,3},则“a=3”是“AB”的充分不必要条件;
②“x<0”是“ln(x+1)<0”的必要不充分条件;
③“函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的充要条件;
④“平面向量 与
与 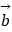 的夹角是钝角”的充要条件的“
的夹角是钝角”的充要条件的“ 
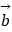 <0”.
<0”.
其中正确命题的序号是(把所有正确命题的序号都写上) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于
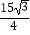 ,D为边长BC上一点.
,D为边长BC上一点. 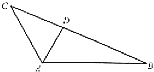
(1)求BC的长;
(2)当AD=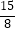 时,求cos∠CAD的值.
时,求cos∠CAD的值.
相关试题

