【题目】计算求值.
(1)已知cosα= ![]() ,α为锐角,求tan2α的值;
,α为锐角,求tan2α的值;
(2)已知sin(θ+ ![]() )=
)= ![]() ,θ为钝角,求cosθ的值.
,θ为钝角,求cosθ的值.
参考答案:
【答案】
(1)∵cosα= ![]() ,α为锐角,
,α为锐角,
∴sinα= ![]() =
= ![]() ,从而可求tan
,从而可求tan ![]() =
= ![]()
∴tan2α= ![]() =
= ![]() =﹣
=﹣ ![]()
(2)∵sin(θ+ ![]() )=
)= ![]() ,θ为钝角,
,θ为钝角,
∴θ+ ![]() ∈(
∈( ![]() ,
, ![]() ),
),
∴cos(θ+ ![]() )=﹣
)=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴cosθ=cos[(θ+ ![]() )﹣
)﹣ ![]() ]
]
=cos(θ+ ![]() )cos
)cos ![]() +sin(θ+
+sin(θ+ ![]() )sin
)sin ![]()
=﹣ ![]() ×
× ![]() +
+ ![]()
=﹣ ![]()
【解析】(1)由已知利用同角三角函数基本关系式可求sinα,进而可求tanα,利用二倍角的正切函数公式即可求tan2α的值.(2)由已知可求范围θ+ ![]() ∈(
∈( ![]() ,
, ![]() ),利用同角三角函数基本关系式可求cos(θ+
),利用同角三角函数基本关系式可求cos(θ+ ![]() )的值,利用θ=(θ+
)的值,利用θ=(θ+ ![]() )﹣
)﹣ ![]() ,根据两角差的余弦函数公式即可计算得解.
,根据两角差的余弦函数公式即可计算得解.
【考点精析】认真审题,首先需要了解两角和与差的余弦公式(两角和与差的余弦公式:![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为备战
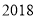 年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得
年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得 分,负者得
分,负者得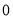 分,在每一场比赛中,甲胜乙的概率为
分,在每一场比赛中,甲胜乙的概率为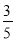 ,丙胜甲的概率为
,丙胜甲的概率为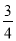 ,乙胜丙的概率为
,乙胜丙的概率为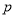 ,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为
,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为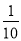 .
.(Ⅰ)求
 的值;
的值;(Ⅱ)设在该次对抗比赛中,丙得分为
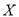 ,求
,求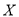 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
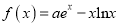 ,其中
,其中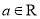 ,
, 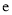 是自然对数的底数.
是自然对数的底数.(Ⅰ)若
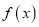 是
是 上的增函数,求
上的增函数,求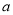 的取值范围;
的取值范围;(Ⅱ)若
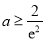 ,证明:
,证明: 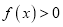 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知点A(2,4),直线l:x﹣2y+1=0.
(1)求过点A且平行于l的直线的方程;
(2)若点M在直线l上,且AM⊥l,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直四棱柱ABCD﹣A1B1C1D1的底面ABCD为菱形,且∠BCD=60°,P为AD1的中点,Q为BC的中点

(1)求证:PQ∥平面D1DCC1;
(2)求证:DQ⊥平面B1BCC1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
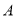 为椭圆
为椭圆 上的一个动点,弦
上的一个动点,弦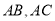 分别过左右焦点
分别过左右焦点 ,且当线段
,且当线段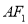 的中点在
的中点在 轴上时,
轴上时, 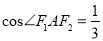 .
.(1)求该椭圆的离心率;(2)设
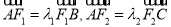 ,试判断
,试判断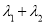 是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2 . (不计木料的粗细与接头处损耗)

(1)如何设计外框的长与宽,才能使外框矩形面积最小?
(2)如何设计外框的长与宽,才能使制作整个展示框所用木条最少?
相关试题

