【题目】如图,在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于 ![]() ,D为边长BC上一点.
,D为边长BC上一点. 
(1)求BC的长;
(2)当AD= ![]() 时,求cos∠CAD的值.
时,求cos∠CAD的值.
参考答案:
【答案】
(1)解:在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于 ![]() ACABsin∠BAC=
ACABsin∠BAC= ![]() 3AB
3AB ![]() =
= ![]() ,
,
∴AB=5,再由余弦定理可得BC2=AB2+AC2﹣2ABACcos∠BAC=25+9﹣2×5×3×(﹣ ![]() )=49,
)=49,
∴BC=7.
(2)解:由题意可得cosC= ![]() =
= ![]() ,sinC=
,sinC= ![]() .
.
D为边长BC上一点,当AD= ![]() 时,△ACD中,利用正弦定理可得
时,△ACD中,利用正弦定理可得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
求得sin∠ADC= ![]() ,∴cos∠ADC=±
,∴cos∠ADC=± ![]() =±
=± ![]() .
.
当 cos∠ADC= ![]() ,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
=﹣ ![]()
![]() +
+ ![]()
![]() =
= ![]() .
.
当 cos∠ADC=﹣ ![]() ,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
=﹣ ![]() (﹣
(﹣ ![]() )+
)+ ![]()
![]() =
= ![]()
【解析】(1)由条件利用余弦定理、三角形的面积公式先求得AB的值,可得BC的值.(2)利用正弦定理求得sin∠ADC 的值,可得cos∠ADC 的值,再利用两角和的余弦公式,求得cos∠CAD=﹣cos(C+∠ADC)的值.
【考点精析】本题主要考查了余弦定理的定义的相关知识点,需要掌握余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
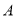 为椭圆
为椭圆 上的一个动点,弦
上的一个动点,弦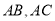 分别过左右焦点
分别过左右焦点 ,且当线段
,且当线段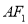 的中点在
的中点在 轴上时,
轴上时, 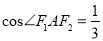 .
.(1)求该椭圆的离心率;(2)设
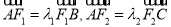 ,试判断
,试判断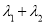 是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2 . (不计木料的粗细与接头处损耗)

(1)如何设计外框的长与宽,才能使外框矩形面积最小?
(2)如何设计外框的长与宽,才能使制作整个展示框所用木条最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①已知集合A={1,a},B={1,2,3},则“a=3”是“AB”的充分不必要条件;
②“x<0”是“ln(x+1)<0”的必要不充分条件;
③“函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的充要条件;
④“平面向量 与
与 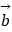 的夹角是钝角”的充要条件的“
的夹角是钝角”的充要条件的“ 
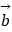 <0”.
<0”.
其中正确命题的序号是(把所有正确命题的序号都写上) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两艘轮船都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随机到达,则这两艘船中至少有一艘在停靠泊位时必须等待的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分14分)如图,已知椭圆
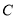 :
: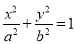 ,其左右焦点为
,其左右焦点为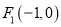 及
及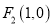 ,过点
,过点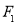 的直线交椭圆
的直线交椭圆 于
于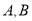 两点,线段
两点,线段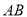 的中点为
的中点为 ,
,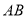 的中垂线与
的中垂线与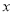 轴和
轴和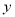 轴分别交于
轴分别交于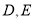 两点,且
两点,且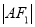 、
、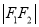 、
、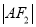 构成等差数列.
构成等差数列.
(1)求椭圆
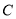 的方程;
的方程;(2)记△
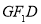 的面积为
的面积为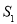 ,△
,△ (
(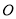 为原点)的面积为
为原点)的面积为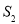 .试问:是否存在直线
.试问:是否存在直线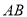 ,使得
,使得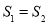 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220.240),[240,260),[260,280),[280,300)分组的频率分布直方图如图.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
相关试题

