【题目】平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右焦点为
的右焦点为![]() ,离心率
,离心率![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为1.
截得的弦长为1.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)记椭圆![]() 的上,下顶点分别为A,B,设过点
的上,下顶点分别为A,B,设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 分别交于点
分别交于点![]() ,求证:直线
,求证:直线![]() 必定过一定点,并求该定点的坐标.
必定过一定点,并求该定点的坐标.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析,定点坐标为
;(Ⅱ)证明见解析,定点坐标为![]() .
.
【解析】试题分析:(Ⅰ)由![]() 及通径
及通径![]() 解方程组求出
解方程组求出![]() 的值即可;(Ⅱ)直线
的值即可;(Ⅱ)直线![]() 方程为:
方程为:
![]() ,直线
,直线![]() 方程为:,即
方程为:,即![]() .分别与椭圆
.分别与椭圆![]() 联立方程组,由韦达定理可解得:
联立方程组,由韦达定理可解得:![]() ,求出直线
,求出直线![]() 的方程化简即可.
的方程化简即可.
试题解析:(Ⅰ)由![]() 可得
可得![]() ,
,
因过点F 垂直于x轴的直线被椭圆所截得弦长为![]() ,
,![]() ,
,
所以![]() ,椭圆
,椭圆![]() 方程为
方程为![]()
(Ⅱ)点![]() 的坐标为
的坐标为![]()
直线![]() 方程为:
方程为:![]() ,直线
,直线![]() 方程为:,即
方程为:,即![]() .
.
分别与椭圆![]() 联立方程组,可得:
联立方程组,可得:
![]()
和![]() ,
,
由韦达定理可解得:
![]() .
.
如果考虑消去![]() ,得到:
,得到:![]() 及
及![]()
进一步亦可得到![]()
直线![]() 的斜率
的斜率![]() ,则直线方程为:
,则直线方程为:![]() ,化简可得直线
,化简可得直线![]() 的方程为
的方程为![]() ,
,
恒过定点![]() .
.
所以直线![]() 必过
必过![]() 轴上的一定点
轴上的一定点![]() .1
.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家,城市缺水尤为突出.某市为了制定合理的节水方案,从该市随机调查了100位居民,获得了他们某月的用水量,整理得到如图的频率分布直方图.
(1)求图中
 的值;
的值;(2)设该市有500万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由:
(3)估计本市居民的月用水量平均数(同一组中的数据用该区间的中点值代表).

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个地区共有5个乡镇,共30万人,其人口比例为3∶2∶5∶2∶3,从这30万人中抽取一个300人的样本,分析某种疾病的发病率.已知这种疾病与不同的地理位置及水土有关,则应采取什么样的抽样方法?并写出具体过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对某电子元件进行寿命追踪调查,情况如下.
寿命(h)
100~200
200~300
300~400
400~500
500~600
个 数
20
30
80
40
30
(1)列出频率分布表,并画出频率分布直方图;
(2)从频率分布直方图估计出电子元件寿命的众数、中位数分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题“等腰三角形的底角必是锐角”,下列假设正确的是( )
A. 等腰三角形的顶角不是锐角 B. 等腰三角形的底角为直角
C. 等腰三角形的底角为钝角 D. 等腰三角形的底角为直角或钝角
-
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={x|-1≤x≤2},B={x|x<1},则A∩B等于( )
A. {x|x<1} B. {x|-1≤x≤2}
C. {x|-1≤x≤1} D. {x|-1≤x<1}
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
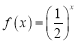 ,函数
,函数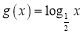 .
.⑴若
 的定义域为
的定义域为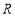 ,求实数
,求实数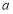 的取值范围;
的取值范围;⑵当
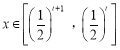 时,求函数
时,求函数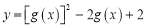 的最小值
的最小值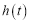 ;
;⑶是否存在非负实数
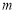 、
、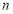 ,使得函数
,使得函数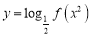 的定义域为
的定义域为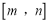 ,值域为
,值域为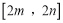 ,若存在,求出
,若存在,求出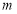 、
、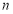 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
相关试题

