【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当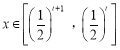 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在非负实数![]() 、
、![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 、
、![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
参考答案:
【答案】⑴![]() ;⑵
;⑵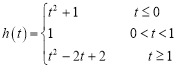 ;⑶存在
;⑶存在![]() 满足题意.
满足题意.
【解析】
试题分析:对问题⑴,根据题目条件首先要对实数![]() 的取值进行分类讨论,再结合极端不等式恒成立即可求出函数
的取值进行分类讨论,再结合极端不等式恒成立即可求出函数![]() 的定义域为
的定义域为![]() 时实数
时实数![]() 的取值范围;对于问题⑵,根据二次函数的单调性并结合对参数
的取值范围;对于问题⑵,根据二次函数的单调性并结合对参数![]() 的分类讨论,即可求得函数
的分类讨论,即可求得函数![]() 的最小值
的最小值![]() ;对问题⑶,根据二次函数的单调性以及函数与方程的思想即可知道存在符合题意的实数
;对问题⑶,根据二次函数的单调性以及函数与方程的思想即可知道存在符合题意的实数![]() 、
、![]() 的值.
的值.
试题解析:⑴![]() 定义域为
定义域为![]() .
.
所以![]() 对一切
对一切![]() 成立. ……………………1分
成立. ……………………1分
当![]() 时,
时,![]() 不可能对一切
不可能对一切![]() 成立. ……………………2分
成立. ……………………2分
所以![]() ,即
,即![]() 解得
解得![]() .
.
综上![]() . ……………………4分
. ……………………4分
⑵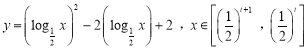 ,
,
令![]() ,
,
所以![]() ……………………5分
……………………5分
当![]() 时,
时,![]() . ……………………6分
. ……………………6分
当![]() 时,
时,![]() . ……………………7分
. ……………………7分
当![]() 时,
时,![]() . ……………………8分
. ……………………8分
所以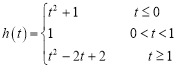 ……………………9分
……………………9分
⑶![]() 在
在![]() 上是增函数,
上是增函数,
若存在非负实数![]() 、
、![]() 满足题意,则
满足题意,则![]() ,………………………………10分
,………………………………10分
即![]() 、
、![]() 是方程
是方程![]() 的两非负实根,且
的两非负实根,且![]() ,
,
所以![]() .
.
即存在![]() 满足题意………………………………12分.
满足题意………………………………12分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系
 中,椭圆
中,椭圆 的右焦点为
的右焦点为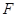 ,离心率
,离心率 ,过点
,过点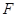 且垂直于
且垂直于 轴的直线被椭圆
轴的直线被椭圆 截得的弦长为1.
截得的弦长为1.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)记椭圆
 的上,下顶点分别为A,B,设过点
的上,下顶点分别为A,B,设过点 的直线
的直线 与椭圆
与椭圆 分别交于点
分别交于点 ,求证:直线
,求证:直线 必定过一定点,并求该定点的坐标.
必定过一定点,并求该定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题“等腰三角形的底角必是锐角”,下列假设正确的是( )
A. 等腰三角形的顶角不是锐角 B. 等腰三角形的底角为直角
C. 等腰三角形的底角为钝角 D. 等腰三角形的底角为直角或钝角
-
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={x|-1≤x≤2},B={x|x<1},则A∩B等于( )
A. {x|x<1} B. {x|-1≤x≤2}
C. {x|-1≤x≤1} D. {x|-1≤x<1}
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题“若a、b∈N,ab能被2整除,则a,b中至少有一个能被2整除”,那么反设的内容是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若0<a<1,b>0则函数f(x)=ax+b的图象一定经过( )
A. 第一、二象限 B. 第二、四象限
C. 第一、二、四象限 D. 第二、三、四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.已知函数
的上界.已知函数 .
.(1)当
 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;(2)若函数
 在
在 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数 的取值范围.
的取值范围.
相关试题

