【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2sin Acos C=2sin B-sin C.
(1)求A的大小;
(2)在锐角三角形ABC中, ![]() ,求c+b的取值范围.
,求c+b的取值范围.
参考答案:
【答案】(1) A=![]() (2) (
(2) (![]() ,2]
,2]
【解析】试题分析:(1) 2sin Acos C=2sin B-sin C.根据内角和![]() 可把sinB换成sin(A+C)展开即得2cos Asin C=sin C,消去sinC,即得cos A=
可把sinB换成sin(A+C)展开即得2cos Asin C=sin C,消去sinC,即得cos A=![]() ,从而得A.(2)根据第一问得出的A=
,从而得A.(2)根据第一问得出的A=![]() ,由正弦定理得出
,由正弦定理得出 ,所以c+b=2sin C+2sin B=2sin B+2sin
,所以c+b=2sin C+2sin B=2sin B+2sin![]() =2sin
=2sin![]() ,由锐角三角形得出
,由锐角三角形得出![]() ,即得解.
,即得解.
试题解析:
(1) ![]() B=π-(A+C),2sin Acos C=2sin B-sin C=2sin Acos C+2cos Asin C-sin C,
B=π-(A+C),2sin Acos C=2sin B-sin C=2sin Acos C+2cos Asin C-sin C, ![]() 2cos Asin C=sin C.
2cos Asin C=sin C. ![]() sin C≠0,
sin C≠0, ![]() cos A=
cos A=![]() .
.
由A∈(0,π),可得A=![]() .
.
(2) ![]() 在锐角三角形ABC中,
在锐角三角形ABC中, ![]() 由(1)可得A=
由(1)可得A=![]() ,B+C=
,B+C=![]()
∴由正弦定理可得:  ,∴c+b=2sin C+2sin B=2sin B+2sin
,∴c+b=2sin C+2sin B=2sin B+2sin![]() =3sin B+
=3sin B+![]() cos B=2sin
cos B=2sin![]() .
. 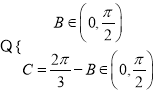 ,可得
,可得![]() ,
, ![]() ,sin
,sin![]()
 可得b+c=2sin
可得b+c=2sin![]() ∈(
∈(![]() ,2].
,2].
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)的定义域为D,若x∈D,y∈D,使得f(y)=﹣f(x)成立,则称函数f(x)为“美丽函数”.下列所给出的五个函数: ①y=x2;②y=
 ;③f(x)=ln(2x+3);④y=2x+3;⑤y=2sin x﹣1.
;③f(x)=ln(2x+3);④y=2x+3;⑤y=2sin x﹣1.
其中是“美丽函数”的序号有 . -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 cos(
cos( 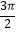 ﹣2x)的单调递增区间是( )
﹣2x)的单调递增区间是( )
A.[kπ﹣ ,kπ+
,kπ+  ](k∈Z)
](k∈Z)
B.[kπ﹣ ,kπ)(k∈Z)
,kπ)(k∈Z)
C.[kπ+ ,kπ+
,kπ+  ](k∈Z)
](k∈Z)
D.[kπ+ ,kπ+π](k∈Z)
,kπ+π](k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值ξ(元)的概率分布列和期望Eξ. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为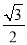 ,点
,点 ,
, 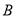 ,
,  分别为椭圆的右顶点、上顶点和右焦点,且
分别为椭圆的右顶点、上顶点和右焦点,且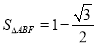 .
.(1)求椭圆
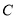 的方程;
的方程;(2)已知直线
 :
: 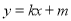 被圆
被圆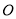 :
: 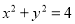 所截得的弦长为
所截得的弦长为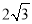 ,若直线
,若直线 与椭圆
与椭圆 交于
交于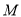 ,
, 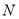 两点,求
两点,求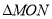 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是
 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(1)从A中又放回的摸球,每次摸出一个,共摸5次 ①恰好有3次摸到红球的概率;
②第一次、第三次、第五次摸到红球的概率.
(2)若A、B两个袋子中的球之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是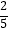 ,求p的值.
,求p的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
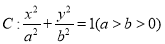 短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为
短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为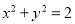 .
. (1)求椭圆
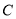 的方程;
的方程;(2)若抛物线
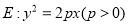 的焦点与椭圆
的焦点与椭圆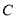 的一个焦点
的一个焦点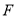 重合,直线
重合,直线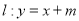 与抛物线
与抛物线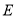 交于两点
交于两点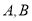 ,且
,且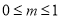 ,求
,求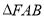 的面积的最大值.
的面积的最大值.
相关试题

