【题目】徐州市为加快新老城区的融合并进一步缓解交通压力,现经过食品城至新城区(昆仑大道)和食品城至高速入口(迎宾大道),分别修建地铁2号线和快速通道,如图,已知两条公路夹角为60°,为了便于施工拟在两条公路之间的区域内建一混凝土搅拌站P,并分别在两条公路边上建两个中转站M、N (异于点A),要求PM=PN=MN=2(单位:千米).![]()
(1) ![]()
(2)问![]() 为多大时,使得混凝土搅拌站产生的噪声对食品城的影响最小(即搅拌站与食品城的距离最远).
为多大时,使得混凝土搅拌站产生的噪声对食品城的影响最小(即搅拌站与食品城的距离最远).

参考答案:
【答案】(1)见解析;(2)设计∠AMN为60时,混凝土搅拌站产生的噪声对食品城的影响最小.
【解析】试题分析:(1)根据正弦定理,即可θ表示AM;(2)根据三角函数的图象和性质,即可求出函数的最值.
试题解析:
(1)因为∠AMN=θ,在△AMN中,![]() =
=![]() .
.
因为MN=2,所以AM=![]() sin(120°-θ) .
sin(120°-θ) . ![]()
(2)在△APM中,cos∠AMP=cos(60°+θ).
由(1)知AM=![]() sin(120°-θ)
sin(120°-θ)
所以AP2=AM2+MP2-2 AM·MP·cos∠AMP
=![]() sin2(120°-θ)+4-2×2×
sin2(120°-θ)+4-2×2×![]() sin(120°-θ) cos(60°+θ)
sin(120°-θ) cos(60°+θ)
=![]() sin2(θ+60°)-
sin2(θ+60°)-![]() sin(θ+60°) cos(θ+60°)+4
sin(θ+60°) cos(θ+60°)+4
=![]() [1-cos (2θ+120°)]-
[1-cos (2θ+120°)]-![]() sin(2θ+120°)+4…
sin(2θ+120°)+4…
=-![]() [
[![]() sin(2θ+120°)+cos (2θ+120°)]+
sin(2θ+120°)+cos (2θ+120°)]+![]()
=![]() -
-![]() sin(2θ+150°),θ∈(0,120°).
sin(2θ+150°),θ∈(0,120°).
当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP取得最大值2![]() .
.
答:设计∠AMN为60时,混凝土搅拌站产生的噪声对食品城的影响最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为
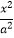 +
+ 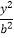 =1(a>b>0),双曲线
=1(a>b>0),双曲线 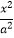 ﹣
﹣ 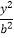 =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 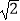 .
.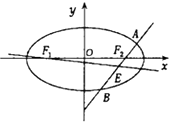
(1)求椭圆C的方程;
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=xlnx+ax,a∈R.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若对x>1,f(x)>(b+a﹣1)x﹣b恒成立,求整数b的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差不为0的等差数列{an}的前n项和为Sn,满足S3=a4+4,且a2,a6,a18成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=
 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的可导函数f(x)的导函数为f'(x),满足f'(x)<f(x),且f(x+3)为偶函数,f(6)=1,则不等式f(x)>ex的解集为( )
A.(﹣∞,0)
B.(0,+∞)
C.(1,+∞)
D.(4,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为
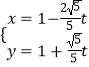 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为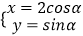 (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为  ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+ax2+bx在x=﹣
 与x=1处都取得极值.
与x=1处都取得极值.
(1)求a,b的值;
(2)求曲线y=f(x)在x=2处的切线方程.
相关试题

