【题目】已知函数f(x)=x3+ax2+bx在x=﹣ ![]() 与x=1处都取得极值.
与x=1处都取得极值.
(1)求a,b的值;
(2)求曲线y=f(x)在x=2处的切线方程.
参考答案:
【答案】
(1)解:f(x)=x3+ax2+bx,f′(x)=3x2+2ax+b,
由f′( ![]() )=
)= ![]() ﹣
﹣ ![]() a+b=0,f′(1)=3+2a+b=0,
a+b=0,f′(1)=3+2a+b=0,
得a=﹣ ![]() ,b=﹣2,
,b=﹣2,
经检验,a=﹣ ![]() ,b=﹣2符合题意;
,b=﹣2符合题意;
(2)解:由(1)得f′(x)=3x2﹣x﹣2,
曲线y=f(x)在x=2处的切线方程斜率k=f′(2)=8,
又∵f(2)=2,
∴曲线y=f(x)在x=2处的切线方程为y﹣2=8(x﹣2),
即8x﹣y﹣14=0为所求.
【解析】(1)先求出函数f(x)的导数,再建立关于a,b的方程组,解方程组可得a,b的值;(2)先求出函数f(x)的导数,再计算f′(2),f(2),进而可得切线方程.
【考点精析】关于本题考查的函数的极值与导数,需要了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】徐州市为加快新老城区的融合并进一步缓解交通压力,现经过食品城至新城区(昆仑大道)和食品城至高速入口(迎宾大道),分别修建地铁2号线和快速通道,如图,已知两条公路夹角为60°,为了便于施工拟在两条公路之间的区域内建一混凝土搅拌站P,并分别在两条公路边上建两个中转站M、N (异于点A),要求PM=PN=MN=2(单位:千米).

(1)

(2)问
 为多大时,使得混凝土搅拌站产生的噪声对食品城的影响最小(即搅拌站与食品城的距离最远).
为多大时,使得混凝土搅拌站产生的噪声对食品城的影响最小(即搅拌站与食品城的距离最远).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的可导函数f(x)的导函数为f'(x),满足f'(x)<f(x),且f(x+3)为偶函数,f(6)=1,则不等式f(x)>ex的解集为( )
A.(﹣∞,0)
B.(0,+∞)
C.(1,+∞)
D.(4,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为
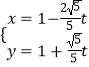 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为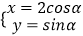 (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为  ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业招聘中,依次进行A科、B科考试,当A科合格时,才可考B科,且两科均有一次补考机会,两科都合格方通过.甲参加招聘,已知他每次考A科合格的概率均为
 ,每次考B科合格的概率均为
,每次考B科合格的概率均为  .假设他不放弃每次考试机会,且每次考试互不影响.
.假设他不放弃每次考试机会,且每次考试互不影响.
(I)求甲恰好3次考试通过的概率;
(II)记甲参加考试的次数为ξ,求ξ的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 数列
数列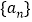 的前
的前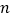 项和,对任意
项和,对任意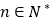 ,都有
,都有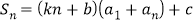 (
(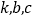 为常数).
为常数).(1)当
 时,求
时,求 ;
;(2)当
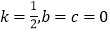 时,
时,(ⅰ)求证:数列
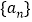 是等差数列;
是等差数列;(ⅱ)若对任意
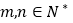 ,必存在
,必存在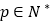 使得
使得 ,已知
,已知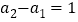 ,且
,且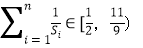 ,
,求数列
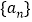 的通项公式.
的通项公式.
相关试题

