【题目】设函数f(x)=xlnx+ax,a∈R.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若对x>1,f(x)>(b+a﹣1)x﹣b恒成立,求整数b的最大值.
参考答案:
【答案】
(1)解:a=1时,f(x)=xlnx+x(x>0).f(1)=1.
f′(x)=lnx+2,f′(1)=2.
∴曲线y=f(x)在点(1,f(1))处的切线方程为:y﹣1=2(x﹣1),
化为:2x﹣y﹣1=0.
(2)解:对x>1,f(x)>(b+a﹣1)x﹣b恒成立,b< ![]() .
.
令g(x)= ![]() ,则g′(x)=
,则g′(x)= ![]() =
= ![]() .
.
令h(x)=x﹣lnx﹣2,x>1.
h′(x)=1﹣ ![]() >0,可知:函数h(x)在(1,+∞)上单调递增.
>0,可知:函数h(x)在(1,+∞)上单调递增.
∴h(x)>h(1)=﹣1,
因此函数h(x)存在唯一零点x0∈(3,4),x0﹣lnx0﹣2=0.
使得g(x)在(1,x0)上单调递减,在(x0,+∞)上单调递增.
∴x=x0时,函数g(x)取得极小值即最小值,
∴b< ![]() =
= ![]() =x0.
=x0.
因此整数b的最大值为3
【解析】(1)a=1时,f(x)=xlnx+x(x>0).f(1)=1.f′(x)=lnx+2,f′(1)=2.利用点斜式即可得出.(2)对x>1,f(x)>(b+a﹣1)x﹣b恒成立,b< ![]() .令g(x)=
.令g(x)= ![]() ,则g′(x)=
,则g′(x)= ![]() =
= ![]() .令h(x)=x﹣lnx﹣2,x>1.L利用导数可知:函数h(x)在(1,+∞)上单调递增.h(x)>h(1)=﹣1,因此函数h(x)存在唯一零点x0∈(3,4),x0﹣lnx0﹣2=0.可得x=x0时,函数g(x)取得极小值即最小值,代入可得b<x0.即可得出.
.令h(x)=x﹣lnx﹣2,x>1.L利用导数可知:函数h(x)在(1,+∞)上单调递增.h(x)>h(1)=﹣1,因此函数h(x)存在唯一零点x0∈(3,4),x0﹣lnx0﹣2=0.可得x=x0时,函数g(x)取得极小值即最小值,代入可得b<x0.即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( >0,
>0,  ≠1,
≠1,  ≠﹣1),是定义在(﹣1,1)上的奇函数.
≠﹣1),是定义在(﹣1,1)上的奇函数.(1)求实数
 的值;
的值;(2)当
 =1时,判断函数
=1时,判断函数 在(﹣1,1)上的单调性,并给出证明;
在(﹣1,1)上的单调性,并给出证明;(3)若
 且
且 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为
 +
+  =1(a>b>0),双曲线
=1(a>b>0),双曲线  ﹣
﹣  =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4  .
.
(1)求椭圆C的方程;
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
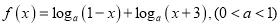 .
.(1)求函数
 的定义域;
的定义域;(2)若函数
 的最小值为
的最小值为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知cos(75°+α)=
 ,α是第三象限角,
,α是第三象限角,(1)求sin(75°+α) 的值.
(2)求cos(α-15°) 的值.
(3)求sin(195°-α)+cos(105o-α)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元.该厂为鼓励销售商定购,决定当一次定购量超过100件时,每多定购一件,订购的全部零件的出厂单价就降低0.02元.根据市场调查,销售商一次定购量不会超过500件.
(1)设一次定购量为x件,服装的实际出厂总价为P元,写出函数P=f(x)的表达式;
(2)当销售商一次定购了450件服装时,该服装厂获得的利润是多少元?
(服装厂售出一件服装的利润=实际出厂价格-成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心为原点,且与直线
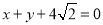 相切.
相切.(1)求圆C的方程;
(2)点
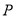 在直线
在直线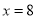 上,过
上,过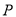 点引圆C的两条切线
点引圆C的两条切线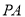 ,
, 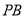 ,切点为
,切点为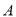 ,
, 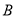 ,求证:直线
,求证:直线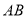 恒过定点.
恒过定点.
相关试题

