【题目】
已知![]() 是递增数列,其前
是递增数列,其前![]() 项和为
项和为![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项
的通项![]() ;
;
(Ⅱ)是否存在![]() 使得
使得![]() 成立?若存在,写出一组符合条件的
成立?若存在,写出一组符合条件的![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)设![]() ,若对于任意的
,若对于任意的![]() ,不等式
,不等式
![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() (2)不存在(3)8
(2)不存在(3)8
【解析】
(Ⅰ)![]() ,得
,得![]() ,解得
,解得![]() ,或
,或![]() .
.
由于![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
故![]() ,
,
整理,得![]() ,即
,即![]() .
.
因为![]() 是递增数列,且
是递增数列,且![]() ,故
,故![]() ,因此
,因此![]() .
.
则数列![]() 是以2为首项,
是以2为首项,![]() 为公差的等差数列.
为公差的等差数列.
所以![]() .………………………………………………5分
.………………………………………………5分
(Ⅱ)满足条件的正整数![]() 不存在,证明如下:
不存在,证明如下:
假设存在![]() ,使得
,使得![]() ,
,
则![]() .
.
整理,得![]() , ①
, ①
显然,左边为整数,所以①式不成立.
故满足条件的正整数![]() 不存在. ……………………8分
不存在. ……………………8分
(Ⅲ)![]() ,
,
不等式![]() 可转化为
可转化为
![]()
![]()
![]() .
.
设![]() ,
,
则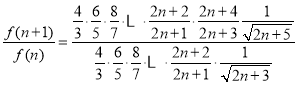
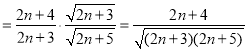
![]() .
.
所以![]() ,即当
,即当![]() 增大时,
增大时,![]() 也增大.
也增大.
要使不等式![]() 对于任意的
对于任意的![]() 恒成立,只需
恒成立,只需![]() 即可.
即可.
因为![]() ,所以
,所以![]() .
.
即![]() .
.
所以,正整数![]() 的最大值为8. ………………………………………14分
的最大值为8. ………………………………………14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
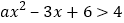 的解集为
的解集为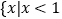 或
或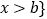 .
.(1)求
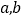 ;(2)解关于
;(2)解关于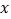 的不等式
的不等式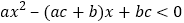
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.则函数y=f(x)( )
A.有极小值,无极大值
B.有极大值,无极小值
C.既有极小值又有极大值
D.既无极小值又无极大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】《张丘建算经》是公元5世纪中国古代内容丰富的数学著作,书中卷上第二十三问:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”其意思为“有个女子织布,每天比前一天多织相同量的布,第一天织五尺,一个月(按30天计)共织390尺.问:每天多织多少布?”已知1匹=4丈,1丈=10尺,估算出每天多织的布的布约有( )
A.0.55尺
B.0.53尺
C.0.52尺
D.0.5尺 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱锥P﹣ABC中E,F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P﹣ABC的外接球的表面积( )
A.4π
B.6π
C.8π
D.12π -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f(
 )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f(  )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ,kπ+
,kπ+  ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ](k∈Z)
](k∈Z)
C.[kπ+ ,kπ+
,kπ+  ](k∈Z)
](k∈Z)
D.[kπ﹣ ,kπ](k∈Z)
,kπ](k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)若函数
 在其定义域上为单调增函数,求
在其定义域上为单调增函数,求 的取值范围;
的取值范围;(2)记
 的导函数为
的导函数为 ,当
,当 时,证明:
时,证明: 存在极小值点
存在极小值点 ,且
,且 .
.
相关试题

