【题目】已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.则函数y=f(x)( )
A.有极小值,无极大值
B.有极大值,无极小值
C.既有极小值又有极大值
D.既无极小值又无极大值
参考答案:
【答案】A
【解析】解:∵ ![]() =
= ![]() =
= ![]() >0,
>0,
∴ ![]() 在(0,+∞)上是增函数,
在(0,+∞)上是增函数,
∵xf′(x)﹣f(x)=xex ,
∴f′(x)= ![]() +ex ,
+ex ,
∵y=ex在(0,+∞)上是增函数,
∴f′(x)在(0,+∞)上是增函数,
又∵f′(1)=﹣3+e<0,f′(2)=0+e2>0,
故f′(x)在(0,+∞)上先负值,后正值;
故函数y=f(x)有极小值,无极大值,
故选A.
【考点精析】根据题目的已知条件,利用函数的极值与导数的相关知识可以得到问题的答案,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是定义域为
是定义域为 的奇函数.
的奇函数.(1)求实数
 的值并判断函数
的值并判断函数 的单调性;
的单调性;(2)当
 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】驻马店市政府委托市电视台进行“创建森林城市”知识问答活动,市电视台随机对该市15~65岁的人群抽取了
 人,绘制出如图1所示的频率分布直方图,回答问题的统计结果如表2所示.
人,绘制出如图1所示的频率分布直方图,回答问题的统计结果如表2所示.
(1)分别求出
 的值;
的值;(2)从第二、三、四、五组回答正确的人中用分层抽样的方法抽取7人,则从第二、三、四、五组每组回答正确的人中应各抽取多少人?
(3)在(2)的条件下,电视台决定在所抽取的7人中随机选2人颁发幸运奖,求所抽取的人中第二组至少有1人获得幸运奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
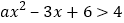 的解集为
的解集为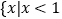 或
或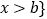 .
.(1)求
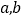 ;(2)解关于
;(2)解关于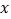 的不等式
的不等式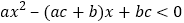
-
科目: 来源: 题型:
查看答案和解析>>【题目】《张丘建算经》是公元5世纪中国古代内容丰富的数学著作,书中卷上第二十三问:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”其意思为“有个女子织布,每天比前一天多织相同量的布,第一天织五尺,一个月(按30天计)共织390尺.问:每天多织多少布?”已知1匹=4丈,1丈=10尺,估算出每天多织的布的布约有( )
A.0.55尺
B.0.53尺
C.0.52尺
D.0.5尺 -
科目: 来源: 题型:
查看答案和解析>>【题目】
已知
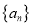 是递增数列,其前
是递增数列,其前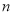 项和为
项和为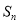 ,
,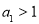 ,且
,且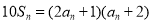 ,
,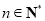 .
.(Ⅰ)求数列
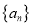 的通项
的通项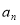 ;
;(Ⅱ)是否存在
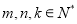 使得
使得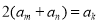 成立?若存在,写出一组符合条件的
成立?若存在,写出一组符合条件的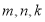 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(Ⅲ)设
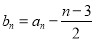 ,若对于任意的
,若对于任意的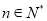 ,不等式
,不等式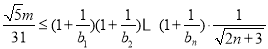 恒成立,求正整数
恒成立,求正整数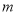 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱锥P﹣ABC中E,F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P﹣ABC的外接球的表面积( )
A.4π
B.6π
C.8π
D.12π
相关试题

