【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在其定义域上为单调增函数,求
在其定义域上为单调增函数,求![]() 的取值范围;
的取值范围;
(2)记![]() 的导函数为
的导函数为![]() ,当
,当![]() 时,证明:
时,证明:![]() 存在极小值点
存在极小值点![]() ,且
,且![]() .
.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】分析:(1)函数![]() 在
在![]() 上为单调增函数,等价于
上为单调增函数,等价于![]() 对任意
对任意![]() 恒成立,
恒成立,![]() 对任意
对任意![]() 恒成立,只需
恒成立,只需![]() ,
,![]() ,利用导数研究函数的单调性,利用单调性求出函数最大值,从而可得结果;(2)由(1)得
,利用导数研究函数的单调性,利用单调性求出函数最大值,从而可得结果;(2)由(1)得![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() 与
与![]() 同号,令
同号,令![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,![]() 是
是![]() 的极小值点,
的极小值点,![]() .
.
详解:(1)依题意函数![]() 的定义域为
的定义域为![]() 且函数
且函数![]() 在
在![]() 上为单调增函数,
上为单调增函数,
所以![]()
![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 为增函数;当
为增函数;当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
∴当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1)得![]() ,其中
,其中![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() 与
与![]() 同号,
同号,
令![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴当![]() 时,
时,![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,
上单调递增,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴存在![]() ,使得
,使得![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() ,
,![]() 是减函数,
是减函数,
∴当![]() 时,
时,![]() ,
,![]() ,
,![]() 是增函数,
是增函数,
∴当![]() 时,存在
时,存在![]() ,使
,使![]() 是
是![]() 的极小值点.
的极小值点.
又由![]() 得
得![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
已知
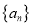 是递增数列,其前
是递增数列,其前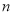 项和为
项和为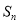 ,
,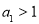 ,且
,且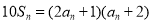 ,
,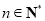 .
.(Ⅰ)求数列
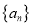 的通项
的通项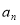 ;
;(Ⅱ)是否存在
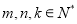 使得
使得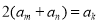 成立?若存在,写出一组符合条件的
成立?若存在,写出一组符合条件的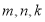 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(Ⅲ)设
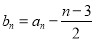 ,若对于任意的
,若对于任意的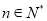 ,不等式
,不等式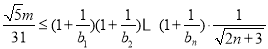 恒成立,求正整数
恒成立,求正整数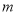 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱锥P﹣ABC中E,F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P﹣ABC的外接球的表面积( )
A.4π
B.6π
C.8π
D.12π -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f(
 )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f(  )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ,kπ+
,kπ+  ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ](k∈Z)
](k∈Z)
C.[kπ+ ,kπ+
,kπ+  ](k∈Z)
](k∈Z)
D.[kπ﹣ ,kπ](k∈Z)
,kπ](k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.则函数y=f(x)( )
A.有极小值,无极大值
B.有极大值,无极小值
C.既有极小值又有极大值
D.既无极小值又无极大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】若数列{an}前n项和为Sn , a1=a2=2,且满足Sn+Sn+1+Sn+2=3n2+6n+5,则S47等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数列{an}前n项和为Sn , a1=a2=2,且满足Sn+Sn+1+Sn+2=3n2+6n+5,则S47等于 .
相关试题

