【题目】已知双曲线![]() ,抛物线
,抛物线![]() ,
, ![]() 与
与![]() 有公共的焦点
有公共的焦点![]() ,
, ![]() 与
与![]() 在第一象限的公共点为
在第一象限的公共点为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,且
,且![]() ,则关于双曲线的离心率的说法正确的是()
,则关于双曲线的离心率的说法正确的是()
A. 仅有两个不同的离心率![]() 且
且![]() B. 仅有两个不同的离心率
B. 仅有两个不同的离心率![]() 且
且![]() C. 仅有一个离心率
C. 仅有一个离心率![]() 且
且![]() D. 仅有一个离心率
D. 仅有一个离心率![]() 且
且![]()
参考答案:
【答案】C
【解析】![]() 的焦点为
的焦点为![]() ,
, ![]() 双曲线交点为
双曲线交点为![]() ,即
,即![]() ,设
,设![]() 横坐标为
横坐标为![]() ,则
,则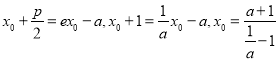 ,
, 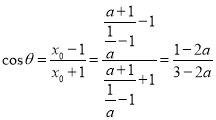 ,
,
可化为![]() ,
, ![]() ,
,
![]() 只有一个根在
只有一个根在![]() 内,故选C.
内,故选C.
【方法点晴】本题主要考查利用双曲线的简单性质求双曲线的离心率,属于中档题.求解与双曲线性质有关的问题时要结合图形进行分析,既使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.求离心率问题应先将 ![]() 用有关的一些量表示出来,再利用其中的一些关系构造出关于
用有关的一些量表示出来,再利用其中的一些关系构造出关于![]() 的等式,从而求出
的等式,从而求出![]() 的值.本题是利用点到直线的距离等于圆半径构造出关于
的值.本题是利用点到直线的距离等于圆半径构造出关于![]() 的等式,最后解出
的等式,最后解出![]() 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=3ax2+2bx+c,且有a+b+c=0,f(0)>0,f(1)>0.
(Ⅰ)求证:a>0,且﹣2<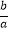 <﹣1;
<﹣1;
(Ⅱ)求证:函数y=f(x)在区间(0,1)内有两个不同的零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:若x>0,则函数y=x+
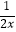 的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
的最小值为1,命题q:若x>1,则x2+2x﹣3>0,则下列命题是真命题的是( )
A.p∨q
B.p∧q
C.(¬p)∧(¬q)
D.p∨(¬q) -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6
B.57.2,56.4
C.62.8,63.6
D.62.8,3.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号
分组
回答正确的人数
回答正确的人数占本组的比例
第1组
[18,28)
5
0.5
第2组
[28,38)
18
a
第3组
[38,48)
27
0.9
第4组
[48,58)
x
0.36
第5组
[58,68)
3
0.2
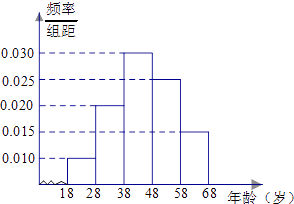
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的方程为
 :
: 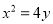 ,过点
,过点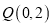 的一条直线与抛物线
的一条直线与抛物线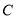 交于
交于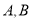 两点,若抛物线在
两点,若抛物线在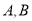 两点的切线交于点
两点的切线交于点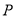 .
.(1)求点
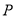 的轨迹方程;
的轨迹方程;(2)设直线
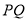 的斜率存在,取为
的斜率存在,取为 ,取直线
,取直线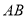 的斜率为
的斜率为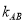 ,请验证
,请验证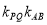 是否为定值?若是,计算出该值;若不是,请说明理由.
是否为定值?若是,计算出该值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件)
产品B(件)
研制成本、搭载费用之和(万元)
20
30
计划最大资金额300万元
产品重量(千克)
10
5
最大搭载重量110千克
预计收益(万元)
80
60
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
相关试题

