【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且在
,且在![]() 轴上的顶点分别为
轴上的顶点分别为![]() ,
,![]() .
.
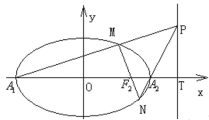
(1)求椭圆的方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为直线
为直线![]() 上异于点
上异于点![]() 的任一点,直线
的任一点,直线![]() 分别与椭圆交于
分别与椭圆交于![]() 点,试问直线
点,试问直线![]() 能否通过椭圆的焦点?若能,求出
能否通过椭圆的焦点?若能,求出![]() 的值,若不能,说明理由.
的值,若不能,说明理由.
参考答案:
【答案】(1)![]() ;(2)能,
;(2)能,![]()
【解析】
(1)由题意得,![]() ,从而求得
,从而求得![]() 、
、![]() 的值,从而求得椭圆的方程.
的值,从而求得椭圆的方程.
(2)设![]() ,
,![]() ,
,![]() ,
,![]() ,把直线方程代入椭圆的方程解出
,把直线方程代入椭圆的方程解出![]() 点、
点、![]() 点坐标,由直线
点坐标,由直线![]() 与直线
与直线![]() 的交点
的交点![]() 在直线
在直线![]() 上,求出直线
上,求出直线![]() 与
与![]() 轴交点坐标,从而求得线
轴交点坐标,从而求得线![]() 是通过椭圆的焦点的条件.
是通过椭圆的焦点的条件.
解:(1)由已知椭圆![]() 的离心率
的离心率![]() ,
,![]() ,则得
,则得![]() ,
,![]() .从而椭圆的方程为
.从而椭圆的方程为![]() .
.
(2)设![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,由
,由![]() 消
消![]() 整理得
整理得![]()
![]() 和
和![]() 是方程的两个根,
是方程的两个根, ![]() 则
则![]() ,
,![]() ,即点
,即点![]() 的坐标为
的坐标为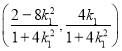 ,
,
同理,设直线![]() 的斜率为
的斜率为![]() ,则得点
,则得点![]() 的坐标为
的坐标为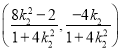
![]() ,
,![]()
![]() ,
,![]() 直线
直线![]() 的方程为:
的方程为:![]() ,
,
![]() 令
令![]() ,得
,得![]() ,将点
,将点![]() 的坐标代入,化简后得:
的坐标代入,化简后得:![]()
又![]() ,
,![]()
![]() 椭圆的焦点为
椭圆的焦点为![]()
![]() ,即
,即![]()
故当![]() 时,
时,![]() 过椭圆的焦点.
过椭圆的焦点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥A-BCD中,AB=a,AC=AD=b,BC=CD=DB=c(a>0,b>0,c>0)该三棱锥的截面EFGH平行于AB、CD,分别交AD、AC、BC、BD于E、F、G、H.

(1)证明:AB⊥CD;
(2)求截面四边形EFGH面积的最大值,并说明面积取最大值时截面的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,直线l过点P(1,2).
(1)若直线l在x轴和y轴上的截距相等,求直线l的方程;
(2)求坐标原点O到直线l距离取最大值时的直线l的方程;
(3)设直线l与x轴正半轴、y轴正半轴分别相交于A,B两点,当|PA||PB|最小时,求直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
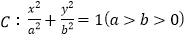 的左焦点为
的左焦点为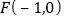 ,离心率
,离心率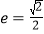 .
.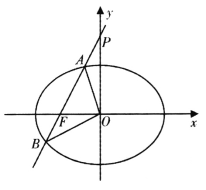
(I)求椭圆C的标准方程;
(II)已知直线
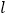 交椭圆C于A,B两点.
交椭圆C于A,B两点.①若直线
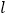 经过椭圆C的左焦点F,交y轴于点P,且满足
经过椭圆C的左焦点F,交y轴于点P,且满足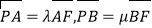 .求证:
.求证: 为定值;
为定值;②若
 ,求
,求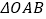 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
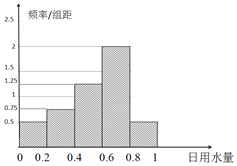
查看答案和解析>>【题目】为达到节水节电的目的,某家庭记录了20天的日用电量xi(单位:度)的频数分布表和这20天相应的日用水量yi(单位:m3)的频率分布直方图如下:
日用电量xi
[0,2)
[2,4)
[4,6)
[6,8)
[8,10)
频数(天)
2
5
7
3
3
(1)假设水费为2.5元/m3,电费为0.6元/度,用以上数据估计该家庭日用电量的平均值和日用水量的平均值,并据此估计该家庭一个月的水费和电费一共是多少?(一个月按30天算,同一组中的数据以这组数据所在区间中点的值作代表);
(2)假设该家庭的日用水量y和日用电量x可用线性回归模型来拟合,请利用(1)中的计算数据及所给的参考数据和公式,建立y与x的回归方程,预测若该家庭日用电量为20度时的日用水量是多少m3?(回归方程的系数小数点后保留2位小数)
参考数据:
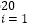 xiyi=65,
xiyi=65,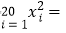 612
612参考公式:回归方程
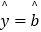 x
x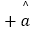 中斜率和截距的公式分别为:
中斜率和截距的公式分别为: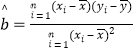 ,
,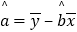
-
科目: 来源: 题型:
查看答案和解析>>【题目】某房地产开发商投资81万元建一座写字楼,第一年装修维护费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元.
(1)若扣除投资和各种装修维护费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案:①纯利润总和最大时,以10万元出售该楼;②年平均利润最大时以46万元出售该楼,问哪种方案更优?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A.在
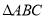 中,
中,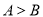 ,
,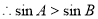
B.在锐角
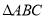 中,不等式
中,不等式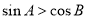 恒成立
恒成立C.在
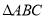 中,若
中,若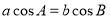 ,则
,则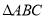 必是等腰直角三角形
必是等腰直角三角形D.在
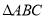 中,若
中,若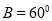 ,
,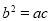 ,则
,则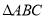 必是等边三角形
必是等边三角形
相关试题

