【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() (
(![]() 是自然常数)时,函数
是自然常数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)当![]() 时,证明:
时,证明:![]() .
.
参考答案:
【答案】(1)![]() ;(2)存在实数a=e2,使得当x∈(0,e]时g(x)有最小值3;(3)详见解析.
;(2)存在实数a=e2,使得当x∈(0,e]时g(x)有最小值3;(3)详见解析.
【解析】
试题分析:(1)首先将问题转化为![]() 在[1,2]上恒成立,然后将其转化为二次函数的图像及其性质即可得出所求的结果;(2)首先假设存在实数a,使g(x)=ax﹣lnx(x∈(0,e])有最小值3,并求出其导函数,然后对其进行分类讨论:①当a≤0时;②当
在[1,2]上恒成立,然后将其转化为二次函数的图像及其性质即可得出所求的结果;(2)首先假设存在实数a,使g(x)=ax﹣lnx(x∈(0,e])有最小值3,并求出其导函数,然后对其进行分类讨论:①当a≤0时;②当![]() 时;③当
时;③当![]() 时,分别利用导数研究函数的单调性并求出其最值即可得出所求的结果;(3)首先令F(x)=e2x﹣lnx,由(2)知,F(x)min,然后令
时,分别利用导数研究函数的单调性并求出其最值即可得出所求的结果;(3)首先令F(x)=e2x﹣lnx,由(2)知,F(x)min,然后令![]() ,并求出其导函数,进而得出其最大值,最后得出不等式成立.
,并求出其导函数,进而得出其最大值,最后得出不等式成立.
试题解析:(1)![]() 在[1,2]上恒成立,
在[1,2]上恒成立,
令h(x)=2x2+ax﹣1,有![]() 得
得 ,得
,得![]() .
.
(2)假设存在实数a,使g(x)=ax﹣lnx(x∈(0,e])有最小值3,![]()
①当a≤0时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae﹣1=3,![]() (舍去),
(舍去),
②当![]() 时,g(x)在
时,g(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
∴![]() ,a=e2,满足条件.
,a=e2,满足条件.
③当![]() 时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae﹣1=3,
时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae﹣1=3,![]() (舍去),
(舍去),
综上,存在实数a=e2,使得当x∈(0,e]时g(x)有最小值3.
(3)令F(x)=e2x﹣lnx,由(2)知,F(x)min=3.令![]() ,
,![]() ,
,
当0<x≤e时,'(x)≥0,φ(x)在(0,e]上单调递增∴![]()
∴![]() ,即
,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市随机抽取一年(365天)内100天的空气质量指数
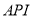 的检测数据,结果统计如下:
的检测数据,结果统计如下: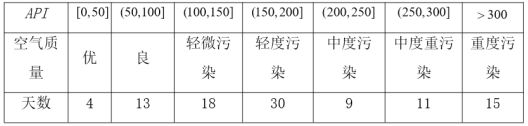
记某企业每天由空气污染造成的经济损失
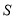 (单位:元),空气质量指数
(单位:元),空气质量指数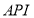 为
为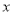 .在区间
.在区间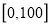 对企业没有造成经济损失;在区间
对企业没有造成经济损失;在区间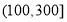 对企业造成经济损失成直线模型(当
对企业造成经济损失成直线模型(当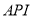 为150时造成的经济损失为500元,当
为150时造成的经济损失为500元,当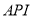 为200时,造成的经济损失为700元);当
为200时,造成的经济损失为700元);当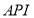 大于300时造成的经济损失为2000元.
大于300时造成的经济损失为2000元.(1)试写出
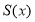 的表达式;
的表达式;(2)试估计在本年内随机抽取一天,该天经济损失
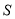 大于200元且不超过600元的概率;
大于200元且不超过600元的概率;(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面
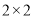 列联表,并判断
列联表,并判断能否有
 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?附:
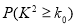
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
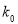
1.32
2.07
2.70
3.74
5.02
6.63
7.87
10.82
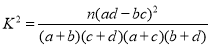
非重度污染
重度污染
合计
供暖季
非供暖季
合计
100
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
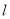 :
: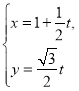 (
(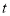 为参数),曲线
为参数),曲线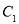 :
: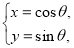 (
(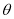 为参数).
为参数).(1)设
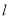 与
与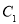 相交于
相交于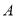 ,
,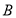 两点,求
两点,求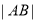 ;
;(2)若把曲线
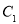 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的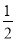 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的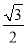 倍,得到曲线
倍,得到曲线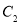 ,设点
,设点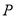 是曲线
是曲线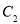 上的一个动点,求它到直线
上的一个动点,求它到直线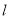 距离的最小值.
距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
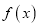 的定义域
的定义域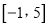 ,部分对应值如表,
,部分对应值如表, 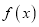 的导函数
的导函数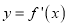 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数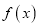 的命题;
的命题;
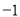
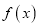
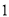
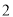
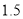

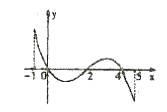
①函数
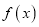 的值域为
的值域为 ;
;②函数
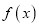 在
在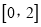 上是减函数;
上是减函数;③如果当
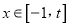 时,
时, 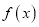 最大值是
最大值是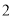 ,那么
,那么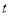 的最大值为
的最大值为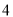 ;
;④当
 时,函数
时,函数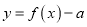 最多有4个零点.
最多有4个零点.其中正确命题的序号是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
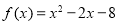 .
.(1)若对
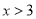 ,不等式
,不等式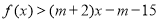 恒成立,求实数
恒成立,求实数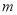 的取值范围;
的取值范围;(2)记
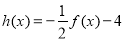 ,那么当
,那么当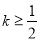 时,是否存在区间
时,是否存在区间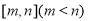 使得函数在区间
使得函数在区间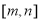 上的值域恰好为
上的值域恰好为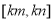 ?若存在,请求出区间
?若存在,请求出区间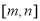 ;若不存在,请说明理由.
;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合
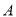 为函数
为函数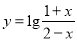 的定义域,集合
的定义域,集合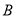 为不等式
为不等式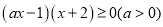 的解集.
的解集.(1)若
 ,求
,求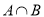 ;
;(2)若
 ,求实数
,求实数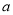 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一段河流,河的一侧是以O为圆心,半径为
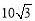 米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧
米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧 的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为
的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为 ,
,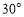 和
和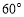 .
.
(1)求烟囱AB的高度;
(2)如果要在CE间修一条直路,求CE的长.
相关试题

