【题目】在△ABC中,内角A,B,C所对的边分别是a,b,c,已知a=2,c= ![]() ,cosA=﹣
,cosA=﹣ ![]() .
.
(1)求sinC和b的值;
(2)求cos(2A+ ![]() )的值.
)的值.
参考答案:
【答案】
(1)解:△ABC中,由cosA=﹣ ![]() 可得sinA=
可得sinA= ![]() .
.
再由 ![]() =
= ![]() 以及a=2、c=
以及a=2、c= ![]() ,可得sinC=
,可得sinC= ![]() .
.
由a2=b2+c2﹣2bccosA 可得b2+b﹣2=0,解得b=1
(2)解:由cosA=﹣ ![]() 、sinA=
、sinA= ![]() 可得 cos2A=2cos2A﹣1=﹣
可得 cos2A=2cos2A﹣1=﹣ ![]() ,sin2A=2sinAcosA=﹣
,sin2A=2sinAcosA=﹣ ![]() .
.
故cos(2A+ ![]() )=cos2Acos
)=cos2Acos ![]() ﹣sin2Asin
﹣sin2Asin ![]() =
= ![]()
【解析】(1)△ABC中,利用同角三角函数的基本关系求出sinA,再由正弦定理求出sinC,再由余弦定理求得b=1.(2)利用二倍角公式求得cos2A的值,由此求得sin2A,再由两角和的余弦公式求出cos(2A+ ![]() )=cos2Acos
)=cos2Acos ![]() ﹣sin2Asin
﹣sin2Asin ![]() 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
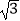 sinxcosx﹣sin2x+
sinxcosx﹣sin2x+  .
.
(1)求f(x)的最小正周期值;
(2)求f(x)的单调递增区间;
(3)求f(x)在[0, ]上的最值及取最值时x的值.
]上的最值及取最值时x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为,且Sn=n2+n,
(1)求数列{an}的通项公式;
(2)令bn=3an , 求证:数列{bn}是等比数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如表:
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?资金
单位产品所需资金(百元)
空调机
洗衣机
月资金供应量(百元)
成本
30
20
300
劳动力(工资)
5
10
110
单位利润
6
8
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为
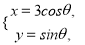 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为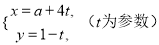 .
.(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为
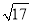 ,求a.
,求a. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,B1C和平面ABCD所成的角的度数为 .
相关试题

