【题目】(1)若抛物线的焦点是椭圆![]() 左顶点,求此抛物线的标准方程;
左顶点,求此抛物线的标准方程;
(2)若某双曲线与椭圆![]() 共焦点,且以
共焦点,且以![]() 为渐近线,求此双曲线的标准方程.
为渐近线,求此双曲线的标准方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)先根据椭圆中的a的值求得c值,从而出左顶点的坐标,再根据抛物线的顶点在坐标原点,焦点是 (-8,0)的位置,求得抛物线方程中的p,抛物线方程可得.
(2)由题意得, ![]() ,48=a2+b2,解出a和b的值,即得所求的双曲线的标准方程.
,48=a2+b2,解出a和b的值,即得所求的双曲线的标准方程.
试题解析:
(1)椭圆![]() 左顶点为(-8,0), 设抛物线的方程为y2=-2px(p>0),可得-
左顶点为(-8,0), 设抛物线的方程为y2=-2px(p>0),可得-![]() =-8,解得p=16,则抛物线的标准方程为
=-8,解得p=16,则抛物线的标准方程为![]() ;
;
(2)椭圆![]() 的焦点为(-4
的焦点为(-4![]() ,0),(4
,0),(4![]() ,0),可设双曲线的方程为
,0),可设双曲线的方程为![]() -
-![]() =1,(a,b>0),则a2+b2=48,由渐近线方程y=±
=1,(a,b>0),则a2+b2=48,由渐近线方程y=±![]() x,可得
x,可得![]() =
=![]() ,解得a=2
,解得a=2![]() ,b=6,则双曲线的方程为
,b=6,则双曲线的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
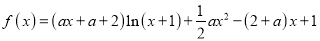 .
.(1)当
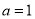 时,判断
时,判断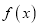 的单调性;
的单调性;(2)若
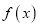 在
在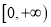 上为单调增函数,求实数
上为单调增函数,求实数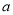 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1)且与x轴有唯一的交点(﹣1,0).
(1)求f(x)的表达式;
(2)在(1)的条件下,设函数F(x)=f(x)﹣mx,若F(x)在区间[﹣2,2]上是单调函数,求实数m的取值范围;
(3)设函数g(x)=f(x)﹣kx,x∈[﹣2,2],记此函数的最小值为h(k),求h(k)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组对象不能构成一个集合的是( )
A.不超过20的非负实数
B.方程x2﹣9=0在实数范围内的解
C.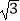 的近似值的全体
的近似值的全体
D.临川十中2016年在校身高超过170厘米的同学的全体 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜三棱柱
 中,侧面
中,侧面 为菱形,底面
为菱形,底面 是等腰直角三角形,
是等腰直角三角形,  .
.
(1)求证:直线
 直线
直线 ;
;(2)若直线
 与底面
与底面 成的角为60°,求二面角
成的角为60°,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面
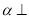 平面
平面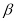 ,
, 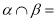 直线
直线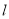 ,
, 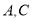 是
是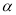 内不同的两点,
内不同的两点, 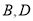 是
是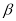 内不同的两点,且
内不同的两点,且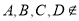 直线
直线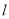 上
上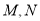 分别是线段
分别是线段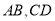 的中点,下列判断正确的是( )
的中点,下列判断正确的是( )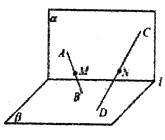
A. 当
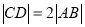 时,
时, 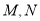 两点不可能重合
两点不可能重合B.
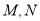 两点可能重合,但此时直线
两点可能重合,但此时直线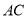 与
与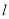 不可能相交
不可能相交C. 当
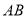 与
与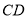 相交,直线
相交,直线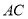 平行于
平行于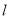 时,直线
时,直线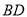 可以与
可以与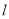 相交
相交D. 当
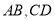 是异面直线时,直线
是异面直线时,直线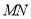 可能与
可能与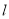 平行
平行 -
科目: 来源: 题型:
查看答案和解析>>【题目】从抛物线y2=32x上各点向x轴作垂线,其垂线段中点的轨迹为E.
(1)求轨迹E的方程;
(2)已知直线l:y=k(x-2)(k>0)与轨迹E交于A,B两点,且点F(2,0),若|AF|=2|BF|,求弦AB的长.
相关试题

