【题目】已知函数![]() .
.
(1)当![]() 时,判断
时,判断![]() 的单调性;
的单调性;
(2)若![]() 在
在![]() 上为单调增函数,求实数
上为单调增函数,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)在![]() 上为增函数;(2)
上为增函数;(2)![]() .
.
【解析】试题分析:(1)当![]() 时,对函数求导后因式分解,根据导数与单调性的知识可写出函数的单调区间.(2)当
时,对函数求导后因式分解,根据导数与单调性的知识可写出函数的单调区间.(2)当![]() 时,可判断函数导数恒为非负数,函数递增符合题意.当
时,可判断函数导数恒为非负数,函数递增符合题意.当![]() 和
和![]() 时,利用函数的二阶导数判断出不符合题意.故
时,利用函数的二阶导数判断出不符合题意.故![]() .
.
试题解析:
(1)当![]() 时,
时, 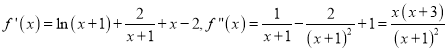 ,所以
,所以![]() 在
在![]() 上为减函数,在
上为减函数,在 ![]() 上为增函数,即
上为增函数,即![]() ,从而可得:
,从而可得: ![]() 在定义域
在定义域 ![]() 上为增函数.
上为增函数.
(2) ①当![]() 时,由于
时,由于![]() ,所以满足
,所以满足![]() 在
在 ![]() 上为单调增函数,即
上为单调增函数,即![]() ;
;
②当![]() 时,
时, ![]()
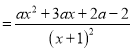 ,由方程
,由方程![]() 的判别式:
的判别式: ![]() ,所以方程有两根
,所以方程有两根![]() ,且由
,且由![]() 知
知![]() ,
, ![]() 在
在![]() 上为减函数,由
上为减函数,由![]() 可知,在
可知,在![]() 时,
时, ![]() ,这与
,这与 ![]() 在
在![]() 上为单调增函数相矛盾. ③ 当
上为单调增函数相矛盾. ③ 当![]() 时,
时, ![]()
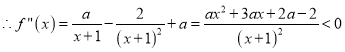 ,
, ![]() 在
在![]() 上为减函数,由
上为减函数,由![]() 可知,在
可知,在![]() 时,
时, ![]() ,这与
,这与 ![]() 在
在![]() 上为单调增函数也是相矛盾. 综上所述:实数
上为单调增函数也是相矛盾. 综上所述:实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲
 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为 万元,且
万元,且 (
( ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为 (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;(2)为了让年利润
 不低于2360万元,求年产量
不低于2360万元,求年产量 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在[﹣1,1]上的奇函数f(x),已知当x∈[﹣1,0]时的解析式f(x)=
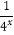 ﹣
﹣ 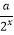 (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高级中学共有学生2000名,各年级男、女生人数如表:

已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求
 的值;
的值;(2)现用分层抽样的方法在全校抽取48名学生,问应该在高三年级抽取多少名?
(3)已知
 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1)且与x轴有唯一的交点(﹣1,0).
(1)求f(x)的表达式;
(2)在(1)的条件下,设函数F(x)=f(x)﹣mx,若F(x)在区间[﹣2,2]上是单调函数,求实数m的取值范围;
(3)设函数g(x)=f(x)﹣kx,x∈[﹣2,2],记此函数的最小值为h(k),求h(k)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组对象不能构成一个集合的是( )
A.不超过20的非负实数
B.方程x2﹣9=0在实数范围内的解
C.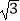 的近似值的全体
的近似值的全体
D.临川十中2016年在校身高超过170厘米的同学的全体 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若抛物线的焦点是椭圆
 左顶点,求此抛物线的标准方程;
左顶点,求此抛物线的标准方程; (2)若某双曲线与椭圆
 共焦点,且以
共焦点,且以 为渐近线,求此双曲线的标准方程.
为渐近线,求此双曲线的标准方程.
相关试题

