【题目】从抛物线y2=32x上各点向x轴作垂线,其垂线段中点的轨迹为E.
(1)求轨迹E的方程;
(2)已知直线l:y=k(x-2)(k>0)与轨迹E交于A,B两点,且点F(2,0),若|AF|=2|BF|,求弦AB的长.
参考答案:
【答案】(1)![]() ;(2)9
;(2)9
【解析】试题分析:(1)先设出垂线段的中点为M(x,y),P(x0,y0)是抛物线上的点,把它们坐标之间的关系找出来,代入抛物线的方程即可;
(2)根据抛物线的方程求出准线方程,利用抛物线的定义即条件,求出A,B的中点横坐标,即可求出弦AB的长.
试题解析:
(1)设垂线段的中点M(x,y),P(x0,y0)是抛物线上的点,D(x0,0),因为M是PD的中点,所以x0=x,y=![]() y0,有x0=x,y0=2y,因为点P在抛物线上,所以y02=32x,即4y2=32x,所以y2=8x,所求点M轨迹方程为:y2=8x.
y0,有x0=x,y0=2y,因为点P在抛物线上,所以y02=32x,即4y2=32x,所以y2=8x,所求点M轨迹方程为:y2=8x.
(2)抛物线y2=8x的焦点坐标为(2,0),准线方程为x=-2,设A(x1,y1),B(x2,y2),则
∵|AF|=2|BF|,∴x1+2=2(x2+2),∴x1=2x2+2∵|y1|=2|y2|,∴x1=4x2,∴x1=4,x2=1,
∴|AB|=x1+x2+p=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若抛物线的焦点是椭圆
 左顶点,求此抛物线的标准方程;
左顶点,求此抛物线的标准方程; (2)若某双曲线与椭圆
 共焦点,且以
共焦点,且以 为渐近线,求此双曲线的标准方程.
为渐近线,求此双曲线的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜三棱柱
 中,侧面
中,侧面 为菱形,底面
为菱形,底面 是等腰直角三角形,
是等腰直角三角形,  .
.
(1)求证:直线
 直线
直线 ;
;(2)若直线
 与底面
与底面 成的角为60°,求二面角
成的角为60°,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面
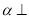 平面
平面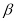 ,
, 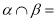 直线
直线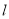 ,
, 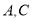 是
是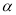 内不同的两点,
内不同的两点, 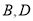 是
是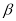 内不同的两点,且
内不同的两点,且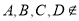 直线
直线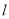 上
上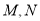 分别是线段
分别是线段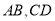 的中点,下列判断正确的是( )
的中点,下列判断正确的是( )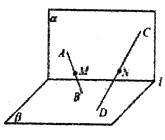
A. 当
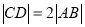 时,
时,  两点不可能重合
两点不可能重合B.
 两点可能重合,但此时直线
两点可能重合,但此时直线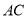 与
与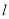 不可能相交
不可能相交C. 当
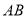 与
与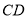 相交,直线
相交,直线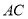 平行于
平行于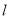 时,直线
时,直线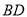 可以与
可以与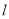 相交
相交D. 当
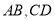 是异面直线时,直线
是异面直线时,直线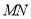 可能与
可能与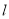 平行
平行 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:实数x满足x2-5ax+4a2<0,其中a>0,命题q:实数x满足
 .
. (1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中表示同一函数的是( )
①f(x)=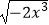 与g(x)=x
与g(x)=x 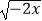
②f(x)=|x|与g(x)=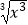
③f(x)=x0与g(x)=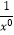
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①③
B.②③
C.③④
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B是抛物线x2=2py(p>0)上的两个动点,O为坐标原点,非零向量
 满足
满足 .
. (1)求证:直线AB经过一定点;
(2)当AB的中点到直线y-2x=0的距离的最小值为
 时,求p的值.
时,求p的值.
相关试题

